7_时间复杂性7.2.ZH

17.2

P 类

定理 7.8 和 7.11 阐明了一个重要的区别。一方面，我们证明了在确定型单带和多带图灵机上测量的问题时间复杂度之间最多只有平方或多项式级别的差异。另一方面，我们展示了在确定型和非确定型图灵机上测量的问题时间复杂度之间最多存在指数级别的差异。

多项式时间

对我们而言，运行时间上的多项式差异被认为是小的，而指数差异被认为是大的。让我们看看

为什么我们选择将这种区分放在多项式和指数之间，而不是放在其他一些函数类别之间。

首先，请注意通常出现的多项式（如 $n^{3}$）和通常出现的指数（如 $2^{n}$）增长率之间的巨大差异。例如，让 $n$ 为 1000，这是算法合理输入的规模。在这种情况下，$n^{3}$ 是 10 亿，这是一个庞大但可管理的数字，而 $2^{n}$ 是一个比宇宙中原子数量大得多的数字。多项式时间算法对于许多目的来说足够快，但指数时间算法却很少有用。

指数时间算法通常在我们通过穷举搜索解决方案空间（称为暴力搜索）来解决问题时出现。例如，将一个数分解为其素因数的一种方法是搜索所有潜在的除数。搜索空间的大小是指数级的，因此这种搜索使用指数时间。有时，通过对问题更深入的理解，可以避免暴力搜索，这可能会揭示一种更实用的多项式时间算法。

所有合理的确定型计算模型都是多项式等价的。也就是说，任何一个模型都可以模拟另一个模型，且运行时间只增加多项式倍。当我们说所有合理的确定型模型都是多项式等价时，我们并不试图定义“合理”。然而，我们设想的这个概念足够广泛，足以包含那些能精确近似实际计算机上运行时间的模型。例如，定理 7.8 表明确定型单带和多带图灵机模型是多项式等价的。

从现在开始，我们专注于时间复杂度理论中不受运行时间上的多项式差异影响的方面。忽略这些差异使我们能够发展一个不依赖于特定计算模型选择的理论。请记住，我们的目标是揭示计算的基本性质，而不是图灵机或任何其他特殊模型的性质。

你可能会觉得忽略运行时间上的多项式差异是荒谬的。真正的程序员当然关心这些差异，并且努力工作只是为了让他们的程序运行速度快两倍。然而，我们早在引入渐近表示法时就忽略了常数因子。现在我们建议忽略更大的多项式差异，例如时间 $n$ 和时间 $n^{3}$ 之间的差异。

我们忽略多项式差异的决定并不意味着我们认为这些差异不重要。相反，我们确实认为时间 $n$ 和时间 $n^{3}$ 之间的差异是一个重要的差异。但是有些问题，例如因数分解问题的多项式性或非多项式性，不依赖于多项式差异，也同样重要。我们只是选择在这里专注于这类问题。为了看清森林而忽略树木，并不意味着一个比另一个更重要——它只是提供了一个不同的视角。

现在我们来介绍复杂度理论中的一个重要定义。

定义 7.12

P 是指在确定型单带图灵机上可在多项式时间内判定的语言类。换句话说，

P 类在我们的理论中扮演着核心角色，并且之所以重要，是因为

1. P 对于所有与确定型单带图灵机多项式等价的计算模型来说都是不变的，并且
2. P 大致对应于在计算机上实际可解决的问题类。

第一点表明 P 是一个数学上稳健的类别。它不受我们所使用的计算模型的具体细节影响。

第二点表明 P 从实践角度来看是相关的。当一个问题属于 P 时，我们有一种在 $n^{k}$ 时间内解决它的方法，其中 $k$ 是某个常数。这种运行时间是否实用取决于 $k$ 和应用程序。当然，$n^{100}$ 的运行时间不太可能具有任何实际用途。然而，将多项式时间称为实际可解决性的门槛已被证明是有用的。一旦为一个以前看似需要指数时间的问题找到了多项式时间算法，就意味着对它有了关键的洞察，并且通常会随后进一步降低其复杂度，常常达到实际有用的程度。

P 中问题的例子

当我们提出一个多项式时间算法时，我们给出它的高级描述，不涉及特定计算模型的特性。这样做可以避免磁带和磁头移动的繁琐细节。我们在描述算法时遵循某些约定，以便能够分析它的多项式性。

我们继续用带编号的阶段来描述算法。现在我们必须对实现每个阶段所需的图灵机步骤数量以及算法使用的总阶段数敏感。

当我们分析一个算法以证明它在多项式时间内运行时，我们需要做两件事。首先，我们必须给出当算法在长度为 $n$ 的输入上运行时所使用的阶段数的多项式上界（通常用大 $O$ 符号表示）。然后，我们必须检查算法描述中的各个阶段，以确保每个阶段都可以在合理的确定型模型上以多项式时间实现。我们在描述算法时选择阶段，以便使这第二部分分析易于进行。当这两项任务都完成后，我们就可以得出结论，该算法在多项式时间内运行，因为我们已经证明它运行了多项式数量的阶段，每个阶段都可以在多项式时间内完成，并且多项式的复合仍然是多项式。

需要注意的一点是问题所使用的编码方法。我们继续使用尖括号表示法 $\langle\cdot\rangle$ 来表示一个或多个对象到字符串的合理编码，而不指定任何特定的编码方法。现在，一种合理的方法是允许以多项式时间将对象编码和解码为自然的内部表示或其他合理的编码。熟悉的图、自动机等编码方法都是合理的。但请注意，用于编码数字的一元表示法（如数字 17 被一元字符串 111111111111111111 编码）不合理，因为它比真正的合理编码（如任何 $k \geq 2$ 的 $k$ 进制表示法）指数级地大。

本章中遇到的许多计算问题都包含图的编码。图的一种合理编码是其节点和边的列表。另一种是邻接矩阵，其中 $(i, j)$ 项为 1 表示从节点 $i$ 到节点 $j$ 有一条边，为 0 则表示没有。当我们分析图上的算法时，运行时间可以根据节点数而不是图表示的大小来计算。在合理的图表示中，表示的大小是节点数的多项式。因此，如果我们分析一个算法并表明其运行时间是节点数的多项式（或指数），我们就知道它是输入大小的多项式（或指数）。

第一个问题涉及有向图。有向图 $G$ 包含节点 $s$ 和 $t$，如下图所示。PATH 问题是确定是否存在从 $s$ 到 $t$ 的有向路径。令

PATH $=\{\langle G, s, t\rangle \mid G$ 是一个有从 $s$ 到 $t$ 的有向路径的有向图$\}$。

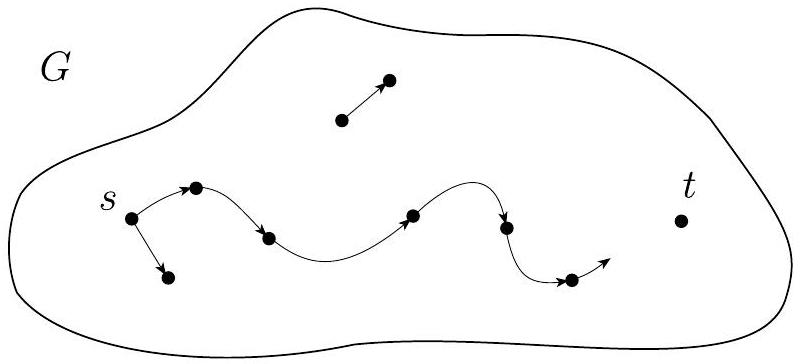
图 7.13

PATH 问题：存在从 $s$ 到 $t$ 的路径吗？

定理 7.14

PATH $\in \mathrm{P}$。

证明思路 我们通过提供一个判定 PATH 的多项式时间算法来证明这个定理。在描述该算法之前，我们先观察一下，解决这个问题的暴力算法不够快。

PATH 的暴力算法通过检查 $G$ 中所有可能的路径来确定是否存在任何从 $s$ 到 $t$ 的有向路径。可能的路径是 $G$ 中长度最多为 $m$ 的节点序列，其中 $m$ 是 $G$ 中的节点数。（如果存在任何从 $s$ 到 $t$ 的有向路径，那么存在一条长度最多为 $m$ 的路径，因为重复节点从来不是必需的。）但是，这类可能的路径的数量大约是 $m^{m}$，这相对于 $G$ 中的节点数是指数级的。因此，这种暴力算法使用指数时间。

为了获得 PATH 的多项式时间算法，我们必须做一些避免暴力搜索的事情。一种方法是使用图搜索方法，例如广度优先搜索。在这里，我们依次标记 $G$ 中所有可以从 $s$ 通过长度为 1、然后 2、然后 3 直到 $m$ 的有向路径到达的节点。将这种策略的运行时间限制在多项式时间内是容易的。

证明 PATH 的多项式时间算法 $M$ 如下操作。

$M=$ “输入 $\langle G, s, t\rangle$，其中 $G$ 是一个带节点 $s$ 和 $t$ 的有向图：

1. 在节点 $s$ 上放置一个标记。
2. 重复以下步骤，直到没有额外的节点被标记：
3. 扫描 $G$ 的所有边。如果发现一条边 $(a, b)$ 从一个已标记的节点 $a$ 到一个未标记的节点 $b$，则标记节点 $b$。
4. 如果 $t$ 被标记，则接受。否则，拒绝。”

现在我们分析这个算法，以证明它在多项式时间内运行。显然，阶段 1 和 4 只执行一次。阶段 3 最多运行 $m$ 次，因为每次（除了最后一次）它都会在 $G$ 中标记一个额外的节点。因此，使用的总阶段数最多为 $1+1+m$，这是一个关于 $G$ 大小的多项式。

$M$ 的阶段 1 和 4 在任何合理的确定型模型上都很容易在多项式时间内实现。阶段 3 涉及对输入的扫描和测试某些节点是否被标记，这也很容易在多项式时间内实现。因此 $M$ 是 PATH 的多项式时间算法。

我们来看另一个多项式时间算法的例子。如果 1 是能同时整除两个数的最大整数，则称这两个数互质。例如，10 和 21 互质，即使它们本身都不是素数，而 10 和 22 不互质，因为它们都可以被 2 整除。令 RELPRIME 是测试两个数是否互质的问题。因此

定理 7.15

RELPRIME $\in \mathrm{P}$。

证明思路 解决这个问题的一种算法是搜索两个数的所有可能的除数，如果没有大于 1 的公除数则接受。然而，以二进制或任何其他 $k \geq 2$ 的 $k$ 进制表示的数的量级，是其表示长度的指数级。因此，这种暴力算法搜索指数数量的潜在除数，并且具有指数运行时间。

相反，我们用一种古老的数值过程，称为欧几里得算法，来计算最大公约数。自然数 $x$ 和 $y$ 的最大公约数，记作 $\operatorname{gcd}(x, y)$，是能同时整除 $x$ 和 $y$ 的最大整数。例如，$\operatorname{gcd}(18,24)=6$。显然，$x$ 和 $y$ 互质当且仅当 $\operatorname{gcd}(x, y)=1$。我们在证明中将欧几里得算法描述为算法 $E$。它使用 $\bmod$ 函数，其中 $x \bmod y$ 是 $x$ 除以 $y$ 的整数除法的余数。

证明 欧几里得算法 $E$ 如下。

$E=$ “输入 $\langle x, y\rangle$，其中 $x$ 和 $y$ 是二进制表示的自然数：

1. 重复直到 $y=0$：
2. 将 $x \leftarrow x \bmod y$ 赋值。
3. 交换 $x$ 和 $y$。
4. 输出 $x$。”

算法 $R$ 使用 $E$ 作为子程序来解决 RELPRIME。

$R=$ “输入 $\langle x, y\rangle$，其中 $x$ 和 $y$ 是二进制表示的自然数：

1. 对 $\langle x, y\rangle$ 运行 $E$。
2. 如果结果是 1，接受。否则，拒绝。”

显然，如果 $E$ 在多项式时间内正确运行，那么 $R$ 也会，因此我们只需要分析 $E$ 的时间和正确性。这个算法的正确性众所周知，所以我们不再讨论。

为了分析 $E$ 的时间复杂度，我们首先证明阶段 2 的每次执行（除了第一次）都会使 $x$ 的值至少减半。执行阶段 2 后，$x<y$，因为 $\bmod$ 函数的性质。执行阶段 3 后，$x>y$，因为两者已交换。因此，当随后执行阶段 2 时，$x>y$。如果 $x / 2 \geq y$，那么 $x \bmod y<y \leq x / 2$，并且 $x$ 至少减半。如果 $x / 2<y$，那么 $x \bmod y=x-y<x / 2$，并且 $x$ 至少减半。

$x$ 和 $y$ 的值在每次执行阶段 3 时都会交换，因此 $x$ 和 $y$ 的原始值在每两次循环中至少都会减半。因此，阶段 2 和 3 执行的最大次数是 $2 \log _{2} x$ 和 $2 \log _{2} y$ 中较小者。这些对数与表示的长度成正比，使得执行的阶段数为 $O(n)$。$E$ 的每个阶段都只使用多项式时间，因此总运行时间是多项式的。

多项式时间算法的最后一个例子表明，每个上下文无关语言都可以在多项式时间内判定。

定理 7.16

每个上下文无关语言都是 P 的成员。

证明思路 在定理 4.9 中，我们证明了每个 CFL 都是可判定的。为此，我们为每个 CFL 提供了一个判定它的算法。如果该算法在多项式时间内运行，则当前定理作为推论成立。让我们回顾一下该算法，并找出它是否运行得足够快。

令 $L$ 是由乔姆斯基范式下的 CFG $G$ 生成的 CFL。根据问题 2.38，任何字符串 $w$ 的推导都有 $2n-1$ 步，其中 $n$ 是 $w$ 的长度，因为 $G$ 处于乔姆斯基范式。当输入是长度为 $n$ 的字符串时，$L$ 的判别器通过尝试所有可能的 $2n-1$ 步推导来工作。如果其中任何一个推导出了 $w$，则判别器接受；否则，它拒绝。

对该算法的快速分析表明它不是在多项式时间内运行的。具有 $k$ 步的推导的数量可能是 $k$ 的指数级，因此该算法可能需要指数时间。

为了获得多项式时间算法，我们引入了一种强大的技术，称为动态规划。该技术利用对较小子问题信息的积累来解决较大的问题。我们记录任何子问题的解决方案，以便我们只需要解决它一次。我们通过制作所有子问题的表格并系统地输入其解决方案来做到这一点。

在这种情况下，我们考虑确定 $G$ 中的每个变量是否生成 $w$ 的每个子字符串的子问题。算法将此子问题的解决方案输入到一个 $n \times n$ 的表格中。对于 $i \leq j$，表格的 $(i, j)$ 项包含生成子字符串 $w_{i} w_{i+1} \cdots w_{j}$ 的变量集合。对于 $i>j$，表格项未使用。

该算法填充 $w$ 的每个子字符串的表格项。首先，它填充长度为 1 的子字符串的项，然后是长度为 2 的子字符串的项，依此类推。

它利用较短长度的项来协助确定较长长度的项。

例如，假设算法已经确定了哪些变量生成了所有长度达 $k$ 的子字符串。为了确定变量 $A$ 是否生成特定长度为 $k+1$ 的子字符串，算法将该子字符串以 $k$ 种可能的方式分成两段非空部分。对于每次分割，算法检查每个规则 $A \rightarrow B C$ 以确定 $B$ 是否生成第一段，$C$ 是否生成第二段，使用之前计算的表格项。如果 $B$ 和 $C$ 都生成了各自的部分，$A$ 则生成该子字符串，因此被添加到相关的表格项中。算法通过检查规则 $A \rightarrow \mathrm{b}$ 的表格，从长度为 1 的字符串开始这个过程。

证明 以下算法 $D$ 实现了该证明思路。令 $G$ 为生成 CFL $L$ 的乔姆斯基范式下的 CFG。假设 $S$ 是开始变量。（回想一下，空字符串在乔姆斯基范式语法中被特殊处理。算法在阶段 1 处理 $w=\varepsilon$ 的特殊情况。）注释出现在双括号内。

$D=$ “输入 $w=w_{1} \cdots w_{n}$：

1. 对于 $w=\varepsilon$，如果 $S \rightarrow \varepsilon$ 是一个规则，则接受；否则，拒绝。$\llbracket w=\varepsilon$ 的情况 $\rrbracket$
2. 对于 $i=1$ 到 $n$：【 检查每个长度为 1 的子字符串 $\rrbracket$
3. 对于每个变量 $A$：
4. 测试 $A \rightarrow \mathrm{b}$ 是否是一个规则，其中 $\mathrm{b}=w_{i}$。
5. 如果是，将 $A$ 放入 table $(i, i)$。
6. 对于 $l=2$ 到 $n$： $\quad \llbracket l$ 是子字符串的长度 $\rrbracket$
7. 对于 $i=1$ 到 $n-l+1$： $\quad \llbracket i$ 是子字符串的起始位置 $\rrbracket$
8. 令 $j=i+l-1$。 $\quad \llbracket j$ 是子字符串的结束位置 $\rrbracket$
9. 对于 $k=i$ 到 $j-1$： $\quad \llbracket k$ 是分割位置 $\rrbracket$
10. 对于每个规则 $A \rightarrow B C$：
11. 如果 table $(i, k)$ 包含 $B$ 且 table $(k+1, j)$ 包含 $C$，将 $A$ 放入 table $(i, j)$。
12. 如果 table $(1, n)$ 包含 $S$，接受；否则，拒绝。”

现在我们分析 $D$。每个阶段都很容易实现在多项式时间内运行。阶段 4 和 5 最多运行 $nv$ 次，其中 $v$ 是 $G$ 中变量的数量，它是一个与 $n$ 无关的固定常数；因此这些阶段运行 $O(n)$ 次。阶段 6 最多运行 $n$ 次。每次阶段 6 运行时，阶段 7 最多运行 $n$ 次。每次阶段 7 运行时，阶段 8 和 9 最多运行 $n$ 次。每次阶段 9 运行时，阶段 10 运行 $r$ 次，其中 $r$ 是 $G$ 的规则数量，它是另一个固定常数。因此，算法的内层循环——阶段 11——运行 $O\left(n^{3}\right)$ 次。总计显示 $D$ 执行了 $O\left(n^{3}\right)$ 个阶段。