17.4 NP-完全性
P 对 NP 问题的重大进展之一发生于20世纪70年代早期,斯蒂芬·库克(Stephen Cook)和列昂尼德·莱文(Leonid Levin)的工作。他们发现了NP中某些问题,其个体复杂度与整个类别的复杂度相关。如果这些问题中的任何一个存在多项式时间算法,那么NP中的所有问题都将是多项式时间可解的。这些问题被称为NP-完全问题。NP-完全性现象无论从理论还是实践角度都非常重要。
从理论方面来看,试图证明 P 不等于 NP 的研究者可以专注于某个NP-完全问题。如果NP中的任何问题需要超过多项式时间,那么NP-完全问题也一样。此外,试图证明 P 等于 NP 的研究者,只需为某个NP-完全问题找到一个多项式时间算法即可实现此目标。
从实践方面来看,NP-完全性现象可以避免浪费时间去寻找一个不存在的解决特定问题的多项式时间算法。尽管我们可能没有必要的数学工具来证明该问题在多项式时间内不可解,但我们相信 P 不等于 NP。因此,证明一个问题是NP-完全的,是其非多项式性的有力证据。
我们介绍的第一个NP-完全问题称为可满足性问题。回想一下,可取值 TRUE 和 FALSE 的变量称为布尔变量(参见0.2节)。通常,我们用 1 表示 TRUE,用 0 表示 FALSE。布尔运算 AND、OR 和 NOT,分别用符号 $\wedge, \vee$, 和 $\neg$ 表示,描述如下。我们用上划线作为 $\neg$ 符号的简写,所以 $\bar{x}$ 表示 $\neg x$。
布尔公式是包含布尔变量和运算的表达式。例如,
就是一个布尔公式。如果存在对变量的0和1赋值能使公式评估为1,则该布尔公式是可满足的。上述公式是可满足的,因为赋值 $x=0, y=1, z=0$ 使 $\phi$ 评估为1。我们称该赋值满足 $\phi$。可满足性问题就是测试一个布尔公式是否可满足。设
现在我们陈述一个定理,它将 SAT 问题的复杂性与 NP 中所有问题的复杂性联系起来。
定理 7.27
$S A T \in \mathrm{P}$ 当且仅当 $\mathrm{P}=\mathrm{NP}$。
接下来,我们阐述该定理证明的核心方法。
多项式时间归约性
在第5章中,我们定义了将一个问题归约到另一个问题的概念。当问题 A 归约到问题 B 时,B 的解可以用来解决 A。现在我们定义一种考虑计算效率的归约性版本。当问题 A 可有效归约到问题 B 时,B 的有效解可以用来有效解决 A。
定义 7.28
函数 $f: \Sigma^{*} \longrightarrow \Sigma^{*}$ 是多项式时间可计算函数,如果存在一个多项式时间图灵机 $M$,当其在任何输入 $w$ 上启动时,只在纸带上输出 $f(w)$ 并停机。
定义 7.29
语言 $A$ 在多项式时间映射归约(或简称为多项式时间归约)到语言 $B$,记作 $A \leq_{\mathrm{P}} B$,如果存在一个多项式时间可计算函数 $f: \Sigma^{*} \longrightarrow \Sigma^{*}$,使得对于每一个 $w$,
函数 $f$ 被称为 A 到 B 的多项式时间归约。
多项式时间归约是第5.3节中定义的映射归约的高效模拟。还有其他形式的高效归约,但多项式时间归约是一种简单形式,足以满足我们的目的,因此我们在此不讨论其他形式。图7.30说明了多项式时间归约。
[^0]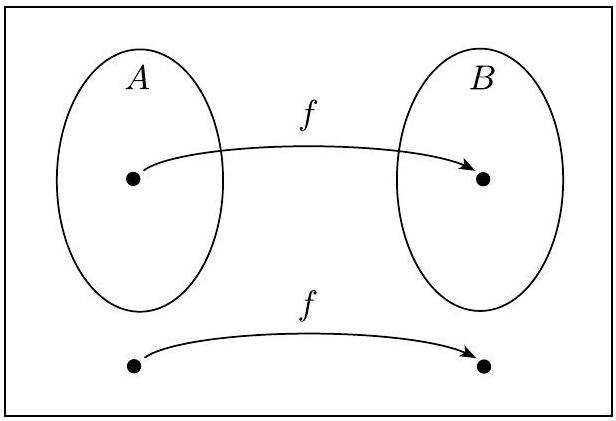
图 7.30
将 A 归约到 B 的多项式时间函数 $f$
与普通映射归约一样,A 到 B 的多项式时间归约提供了一种将 A 中的成员资格测试转换为 B 中的成员资格测试的方法——但现在转换是高效完成的。为了测试 $w \in A$,我们使用归约 $f$ 将 $w$ 映射到 $f(w)$,然后测试 $f(w) \in B$。
如果一种语言可以多项式时间归约到一个已知具有多项式时间解的语言,那么我们就获得了原语言的多项式时间解,如下面的定理所示。
定理 7.31
如果 $A \leq_{\mathrm{P}} B$ 且 $B \in \mathrm{P}$,则 $A \in \mathrm{P}$。
证明 令 $M$ 是决定 B 的多项式时间算法,$f$ 是从 A 到 B 的多项式时间归约。我们描述一个决定 A 的多项式时间算法 $N$ 如下。
$N=$ “在输入 $w$ 上:
- 计算 $f(w)$。
- 在输入 $f(w)$ 上运行 $M$,并输出 $M$ 输出的任何结果。”
由于 $f$ 是从 A 到 B 的归约,所以当 $f(w) \in B$ 时,$w \in A$。因此,$M$ 在 $w \in A$ 时接受 $f(w)$。此外,$N$ 在多项式时间内运行,因为它的两个阶段都在多项式时间内运行。请注意,阶段2在多项式时间内运行,因为两个多项式的复合仍然是多项式。
在演示多项式时间归约之前,我们介绍 3SAT,这是可满足性问题的一个特例,其中所有公式都采用特殊形式。文字是布尔变量或被否定的布尔变量,如 $x$ 或 $\bar{x}$。子句是几个用 $\vee$ 连接的文字,如 $\left(x_{1} \vee \overline{x_{2}} \vee \overline{x_{3}} \vee x_{4}\right)$。布尔公式如果由几个用 $\wedge$ 连接的子句组成,则为合取范式(称为 cnf-公式),如
如果所有子句都包含三个文字,则为 3cnf-公式,如
设 $3 S A T=\{\langle\phi\rangle \mid \phi$ 是一个可满足的 3cnf-公式$\}$。如果一个赋值满足一个 cnf-公式,则每个子句必须至少包含一个评估为 1 的文字。
以下定理介绍了从 3SAT 问题到 CLIQUE 问题的多项式时间归约。
定理 7.32
3SAT 可多项式时间归约到 CLIQUE。
证明思路 我们从 3SAT 到 CLIQUE 演示的多项式时间归约 $f$ 将公式转换为图。在所构建的图中,指定大小的团对应于公式的可满足赋值。图中的结构旨在模拟变量和子句的行为。
证明 设 $\phi$ 是一个包含 $k$ 个子句的公式,例如
归约 $f$ 生成字符串 $\langle G, k\rangle$,其中 $G$ 是一个无向图,定义如下。
$G$ 中的节点被组织成 $k$ 组,每组包含三个节点,称为三元组 $t_{1}, \ldots, t_{k}$。每个三元组对应于 $\phi$ 中的一个子句,每个三元组中的节点对应于相关子句中的一个文字。用 $\phi$ 中对应的文字标记 $G$ 的每个节点。
$G$ 的边连接 $G$ 中除两种类型节点对之外的所有节点对。同一三元组中的节点之间没有边,具有矛盾标签的两个节点之间也没有边,例如 $x_{2}$ 和 $\overline{x_{2}}$。图7.33说明了当 $\phi=\left(x_{1} \vee x_{1} \vee x_{2}\right) \wedge\left(\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{2}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{2}\right)$ 时的这种构造。
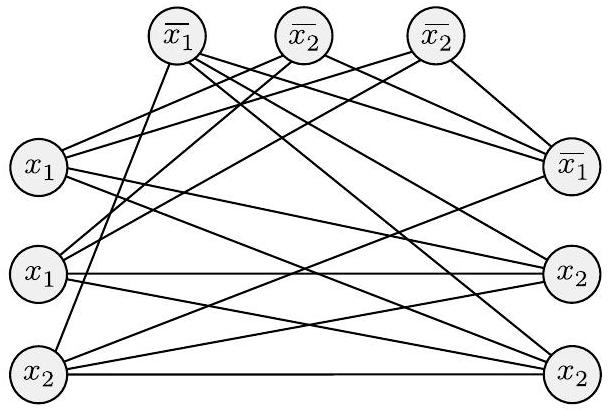
图 7.33
归约从 $\phi=\left(x_{1} \vee x_{1} \vee x_{2}\right) \wedge\left(\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{2}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{2}\right)$ 产生的图
现在我们演示这种构造为何有效。我们证明 $\phi$ 是可满足的当且仅当 $G$ 具有一个 $k$-团。
假设 $\phi$ 有一个可满足赋值。在该可满足赋值中,每个子句中至少有一个文字为真。在 $G$ 的每个三元组中,我们选择一个对应于可满足赋值中真文字的节点。如果特定子句中有多个文字为真,我们任意选择其中一个真文字。刚刚选择的节点形成一个 $k$-团。选择的节点数量为 $k$,因为我们为每个 $k$ 个三元组选择了一个节点。每对选定的节点通过一条边连接,因为没有一对符合前面描述的例外情况。它们不可能来自同一个三元组,因为我们每个三元组只选择一个节点。它们不可能具有矛盾的标签,因为相关文字在可满足赋值中都为真。因此,$G$ 包含一个 $k$-团。
假设 $G$ 有一个 $k$-团。团的任何两个节点都不在同一个三元组中,因为同一个三元组中的节点没有边连接。因此,每个 $k$ 个三元组中正好包含一个 $k$ 个团节点。我们将真值赋给 $\phi$ 的变量,使得标记团节点的每个文字都变为真。这样做总是可能的,因为以矛盾方式标记的两个节点没有边连接,因此不可能都存在于团中。对变量的这个赋值满足 $\phi$,因为每个三元组包含一个团节点,因此每个子句包含一个被赋为真的文字。因此,$\phi$ 是可满足的。
定理 7.31 和 7.32 告诉我们,如果 CLIQUE 可以在多项式时间内解决,那么 3SAT 也可以。乍一看,这两个问题之间的这种联系相当引人注目,因为从表面上看,它们截然不同。但是多项式时间归约性允许我们将它们的复杂性联系起来。现在我们转向一个定义,它将允许我们类似地将一整类问题的复杂性联系起来。
NP-完全性的定义
定义
734
语言 $B$ 是NP-完全的,如果它满足两个条件:
- $B$ 在 NP 中,并且
- NP 中的每个 $A$ 都可多项式时间归约到 $B$。
定理
7.35
如果 $B$ 是NP-完全的且 $B \in \mathrm{P}$,则 $\mathrm{P}=\mathrm{NP}$。
证明 该定理直接遵循多项式时间归约性的定义。
定理
7.36
如果 $B$ 是NP-完全的,并且对于 NP 中的 $C$, $B \leq_{\mathrm{P}} C$,则 $C$ 是NP-完全的。
证明 我们已经知道 $C$ 在 NP 中,所以我们必须证明 NP 中的每个 $A$ 都可多项式时间归约到 $C$。因为 $B$ 是NP-完全的,所以 NP 中的每个语言都可多项式时间归约到 $B$,而 $B$ 又可多项式时间归约到 $C$。多项式时间归约是可复合的;也就是说,如果 $A$ 可多项式时间归约到 $B$ 且 $B$ 可多项式时间归约到 $C$,那么 $A$ 可多项式时间归约到 $C$。因此,NP 中的每个语言都可多项式时间归约到 $C$。
库克-莱文定理
一旦我们有了一个NP-完全问题,我们就可以通过从它进行多项式时间归约来获得其他问题。然而,确定第一个NP-完全问题则更为困难。现在我们通过证明 SAT 是NP-完全的来做到这一点。
定理 7.37
SAT 是NP-完全的。 ${ }^{2}$
该定理蕴含定理7.27。
[^1]证明思路 证明 SAT 在 NP 中很容易,我们很快就会这样做。证明的难点在于证明 NP 中的任何语言都可以多项式时间归约到 SAT。
为此,我们为 NP 中的每个语言 $A$ 构建一个到 SAT 的多项式时间归约。A 的归约接受一个字符串 $w$ 并生成一个布尔公式 $\phi$,该公式模拟 A 的 NP 机器在输入 $w$ 上的运行。如果机器接受,$\phi$ 有一个可满足赋值,对应于接受计算。如果机器不接受,则没有赋值满足 $\phi$。因此,$w$ 在 $A$ 中当且仅当 $\phi$ 是可满足的。
实际构建以这种方式工作的归约是一个概念上简单的任务,尽管我们必须处理许多细节。布尔公式可以包含布尔运算 AND、OR 和 NOT,这些运算构成了电子计算机中使用的电路的基础。因此,我们可以设计一个布尔公式来模拟图灵机这一事实并不令人惊讶。细节在于这个想法的实现。
证明 首先,我们证明 SAT 在 NP 中。一个非确定性多项式时间机器可以猜测给定公式 $\phi$ 的一个赋值,并在赋值满足 $\phi$ 时接受。
接下来,我们取 NP 中的任何语言 $A$,并证明 $A$ 可多项式时间归约到 SAT。令 $N$ 是一个在 $n^{k}$ 时间内决定 $A$ 的非确定性图灵机,其中 $k$ 为某个常数。(为方便起见,我们实际上假设 $N$ 在 $n^{k}-3$ 时间内运行;但只有对细节感兴趣的读者才需要担心这个小问题。)以下概念有助于描述归约。
$N$ 在 $w$ 上的格局表是一个 $n^{k} \times n^{k}$ 的表格,其行是 $N$ 在输入 $w$ 上的计算分支的格局,如下图所示。
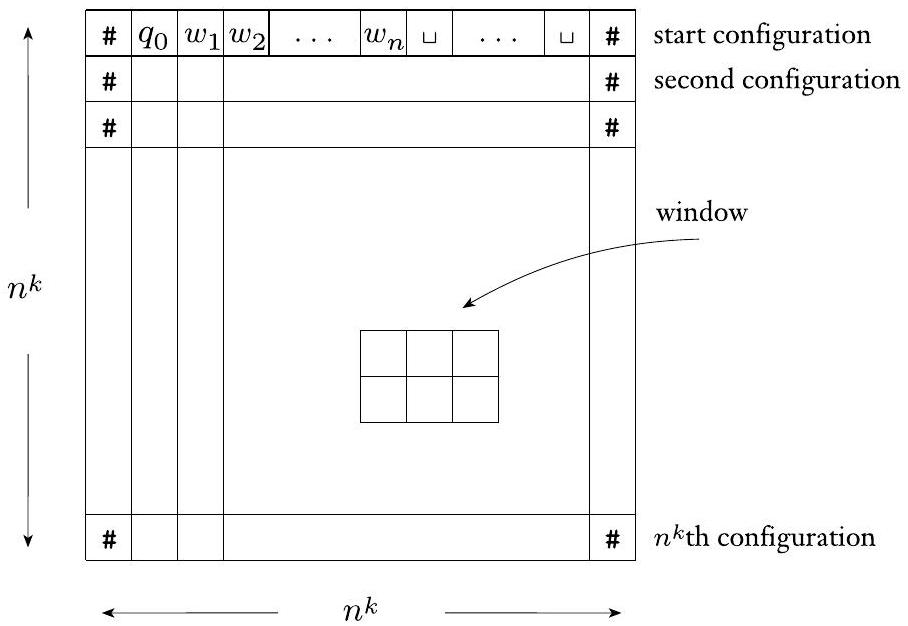
图 7.38
格局表是一个 $n^{k} \times n^{k}$ 的格局表
为方便起见,我们假设每个格局都以 # 符号开始和结束。因此,格局表的第一列和最后一列都是 #。格局表的第一行是 $N$ 在 $w$ 上的起始格局,每行都根据 $N$ 的转移函数紧随前一行。如果格局表的任何一行是接受格局,则该格局表是接受的。
$N$ 在 $w$ 上的每个接受格局表都对应于 $N$ 在 $w$ 上的一个接受计算分支。因此,确定 $N$ 是否接受 $w$ 的问题等价于确定 $N$ 在 $w$ 上是否存在接受格局表的问题。
现在我们来描述从 $A$ 到 SAT 的多项式时间归约 $f$。在输入 $w$ 上,归约生成一个公式 $\phi$。我们首先描述 $\phi$ 的变量。假设 $Q$ 和 $\Gamma$ 分别是 $N$ 的状态集和磁带字母表。令 $C=Q \cup \Gamma \cup\{\#\}$。对于每个介于 1 和 $n^{k}$ 之间的 $i$ 和 $j$,以及 $C$ 中的每个 $s$,我们有一个变量 $x_{i, j, s}$。
格局表的 $\left(n^{k}\right)^{2}$ 个条目中的每一个都称为一个单元格。行 $i$ 和列 $j$ 中的单元格称为单元格 $[i, j]$,包含来自 $C$ 的一个符号。我们用 $\phi$ 的变量表示单元格的内容。如果 $x_{i, j, s}$ 取值 1,则表示单元格 $[i, j]$ 包含一个 $s$。
现在我们设计 $\phi$,使得变量的可满足赋值确实对应于 $N$ 在 $w$ 上的接受格局表。公式 $\phi$ 是四个部分的 AND:$\phi_{\text {cell }} \wedge \phi_{\text {start }} \wedge \phi_{\text {move }} \wedge \phi_{\text {accept }}$。我们依次描述每个部分。
如前所述,将变量 $x_{i, j, s}$ 置为 1 对应于将符号 $s$ 放入单元格 $[i, j]$。为了获得赋值与格局表之间的对应关系,我们必须首先保证赋值为每个单元格只开启一个变量。公式 $\phi_{\text {cell}}$ 通过用布尔运算表达此要求来确保此要求:
符号 $\wedge$ 和 $\vee$ 代表迭代的 AND 和 OR。例如,前面公式中的表达式
是以下内容的简写
其中 $C=\left\{s_{1}, s_{2}, \ldots, s_{l}\right\}$。因此,$\phi_{\text {cell}}$ 实际上是一个大型表达式,其中包含格局表中每个单元格的片段,因为 $i$ 和 $j$ 的范围是从 1 到 $n^{k}$。每个片段的第一部分表示在相应单元格中至少有一个变量被开启。每个片段的第二部分表示在相应单元格中没有超过一个变量被开启(字面意思是,在每对变量中,至少有一个被关闭)。这些片段通过 $\wedge$ 运算连接。
$\phi_{\text {cell}}$ 方括号内的第一部分规定,与每个单元格关联的至少一个变量是开启的,而第二部分规定,每个单元格最多只能有一个变量是开启的。任何满足 $\phi$(因此满足 $\phi_{\text {cell}}$)的变量赋值都必须为每个单元格开启一个变量。因此,任何可满足赋值都指定了表中每个单元格的一个符号。部分 $\phi_{\text {start}} 、 \phi_{\text {move}}$ 和 $\phi_{\text {accept}}$ 确保这些符号实际对应于一个接受格局表,如下所示。
公式 $\phi_{\text {start}}$ 确保表的第一行是 $N$ 在 $w$ 上的起始格局,通过明确规定相应的变量是开启的:
公式 $\phi_{\text {accept}}$ 保证格局表中出现一个接受格局。它通过规定相应的一个变量开启来确保接受状态的符号 $q_{\text {accept}}$ 出现在格局表的一个单元格中:
最后,公式 $\phi_{\text {move}}$ 保证格局表的每一行都对应于一个根据 $N$ 规则合法地跟随前一行的格局。它通过确保每个 $2 \times 3$ 单元格窗口是合法的来做到这一点。我们说一个 $2 \times 3$ 窗口是合法的,如果该窗口不违反 $N$ 的转移函数所指定的操作。换句话说,如果一个窗口可能在一个格局正确地跟随另一个格局时出现,那么该窗口就是合法的。 ${ }^{3}$
例如,假设 a、b 和 c 是磁带字母表的成员,$q_{1}$ 和 $q_{2}$ 是 $N$ 的状态。假设当处于状态 $q_{1}$ 且磁头读取 a 时,$N$ 写入 b,保持状态 $q_{1}$,并向右移动;并且当处于状态 $q_{1}$ 且磁头读取 b 时,$N$ 非确定性地要么
- 写入 c,进入 $q_{2}$,并向左移动,或者
- 写入 a,进入 $q_{2}$,并向右移动。
正式表达为,$\delta\left(q_{1}, \mathrm{a}\right)=\left\{\left(q_{1}, \mathrm{~b}, \mathrm{R}\right)\right\}$ 且 $\delta\left(q_{1}, \mathrm{~b}\right)=\left\{\left(q_{2}, \mathrm{c}, \mathrm{L}\right),\left(q_{2}, \mathrm{a}, \mathrm{R}\right)\right\}$。图7.39显示了该机器的合法窗口示例。
| a | $q_{1}$ | b |
| :---: | :---: | :---: |
| $q_{2}$ | a | c |
(b)
| a | $q_{1}$ | b |
| :---: | :---: | :---: |
| a | a | $q_{2}$ |
(c)
| a | a | $q_{1}$ |
| :---: | :---: | :---: |
| a | a | b |
(d)
| $\#$ | b | a |
| :--- | :--- | :--- |
| $\#$ | b | a |
(e)
| a | b | a |
| :---: | :---: | :---: |
| a | b | $q_{2}$ |
(f)
| b | b | b |
| :---: | :---: | :---: |
| c | b | b |
图 7.39
合法窗口示例
在图7.39中,窗口 (a) 和 (b) 是合法的,因为转移函数允许 $N$ 以指示的方式移动。窗口 (c) 是合法的,因为 $q_{1}$ 出现在顶行的右侧,我们不知道磁头在哪个符号上方。该符号可能是一个 a,并且 $q_{1}$ 可能会将其更改为 b 并向右移动。这种可能性将产生这个窗口,所以它不违反 $N$ 的规则。窗口 (d) 显然是合法的,因为顶部和底部完全相同,这会在磁头不邻近窗口位置时发生。请注意,# 可能出现在合法窗口的顶部和底部的左侧或右侧。窗口 (e) 是合法的,因为状态 $q_{1}$ 读取 b 可能紧邻顶行的右侧,然后它将以状态 $q_{2}$ 向左移动,出现在底行的右端。最后,窗口 (f) 是合法的,因为状态 $q_{1}$ 可能紧邻顶行的左侧,并且它可能将 b 更改为 c 并向左移动。
下图所示的窗口对机器 $N$ 来说是不合法的。
(a)
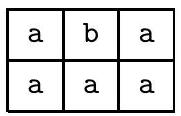
(b)
| a | $q_{1}$ | b |
| :---: | :---: | :---: |
| $q_{2}$ | a | a |
(c)
| b | $q_{1}$ | b |
| :---: | :---: | :---: |
| $q_{2}$ | b | $q_{2}$ |
图 7.40
非法窗口示例
在窗口 (a) 中,顶行的中心符号无法改变,因为状态不与其相邻。窗口 (b) 不合法,因为转移函数规定 b 会变为 c,而不是 a。窗口 (c) 不合法,因为底行出现两个状态。
断言 7.41
如果格局表的顶行是起始格局,并且格局表中的每个窗口都是合法的,则格局表的每一行都是合法地跟随前一行的格局。
我们通过考虑格局表中任意两个相邻的格局来证明此断言,分别称为上层格局和下层格局。在上层格局中,每个包含磁带符号且不邻近状态符号的单元格都是窗口的中心顶部单元格,其顶行不包含任何状态。因此,该符号必须在窗口的中心底部保持不变。因此,它在底部格局中出现在相同的位置。
包含状态符号的窗口在中心顶部单元格中保证了相应的三位置与转移函数一致地更新。因此,如果上层格局是合法格局,那么下层格局也是合法格局,并且下层格局根据 $N$ 的规则跟随上层格局。请注意,尽管这个证明是直接的,但它关键地依赖于我们选择 $2 \times 3$ 的窗口大小,如问题 7.26 所示。
现在我们回到 $\phi_{\text {move}}$ 的构建。它规定格局表中的所有窗口都是合法的。每个窗口包含六个单元格,可以通过固定数量的方式设置以生成合法窗口。公式 $\phi_{\text {move}}$ 表示这六个单元格的设置必须是这些方式之一,或者
$(i, j)$-窗口以单元格 $[i, j]$ 作为中心顶部位置。我们将此公式中的文本 “the $(i, j)$-window is legal” 替换为以下公式。我们将窗口的六个单元格的内容写为 $a_{1}, \ldots, a_{6}$。
接下来,我们分析归约的复杂性,以表明它在多项式时间内运行。为此,我们检查 $\phi$ 的大小。首先,我们估计它拥有的变量数量。回想一下,格局表是一个 $n^{k} \times n^{k}$ 的表格,因此它包含 $n^{2 k}$ 个单元格。每个单元格有 $l$ 个与之关联的变量,其中 $l$ 是 $C$ 中的符号数量。因为 $l$ 仅取决于 TM $N$,而不取决于输入 $n$ 的长度,所以变量总数是 $O\left(n^{2 k}\right)$。
我们估计 $\phi$ 各部分的大小。公式 $\phi_{\text {cell}}$ 包含公式中每个格局表单元格的固定大小片段,因此其大小为 $O\left(n^{2 k}\right)$。公式 $\phi_{\text {start}}$ 包含顶行每个单元格的片段,因此其大小为 $O\left(n^{k}\right)$。公式 $\phi_{\text {move}}$ 和 $\phi_{\text {accept}}$ 都包含公式中每个格局表单元格的固定大小片段,因此它们的大小均为 $O\left(n^{2 k}\right)$。因此,$\phi$ 的总大小为 $O\left(n^{2 k}\right)$。该上限足以满足我们的目的,因为它表明 $\phi$ 的大小是 $n$ 的多项式。如果它不是多项式,那么归约就没有机会在多项式时间内生成它。(实际上,我们的估计由于每个变量都有可能达到 $n^{k}$ 的索引,因此可能需要 $O(\log n)$ 个符号才能写入公式,所以我们的估计偏低了 $O(\log n)$ 的一个因子,但这个额外的因子不会改变结果的多项式性。)
为了说明我们可以在多项式时间内生成公式,请注意其高度重复的性质。公式的每个组件都由许多几乎
完全相同的片段组成,这些片段只在索引方面以简单的方式有所不同。因此,我们可以很容易地构建一个归约,在多项式时间内从输入 $w$ 生成 $\phi$。
至此,我们完成了库克-莱文定理的证明,表明 SAT 是NP-完全的。证明其他语言的NP-完全性通常不需要如此冗长的证明。相反,可以通过从一个已知是NP-完全的语言进行多项式时间归约来证明NP-完全性。我们可以使用 SAT 来达到此目的;但使用 3SAT,即我们在第302页定义的 SAT 的特例,通常会更容易。回想一下,3SAT 中的公式是合取范式(cnf),每个子句包含三个文字。首先,我们必须证明 3SAT 本身是NP-完全的。我们将此断言作为定理 7.37 的推论来证明。
推论 7.42
3SAT 是NP-完全的。
证明 显然 3SAT 在 NP 中,所以我们只需要证明 NP 中的所有语言都可以在多项式时间内归约到 3SAT。一种方法是证明 SAT 可多项式时间归约到 3SAT。相反,我们修改定理 7.37 的证明,使其直接产生一个合取范式且每个子句包含三个文字的公式。
定理 7.37 产生的公式几乎已经是合取范式。公式 $\phi_{\text {cell}}$ 是子公式的大 AND,每个子公式都包含一个大 OR 和一个 OR 的大 AND。因此,$\phi_{\text {cell}}$ 是子句的 AND,因此已经是 cnf 形式。公式 $\phi_{\text {start}}$ 是变量的大 AND。将这些变量中的每一个视为大小为 1 的子句,我们看到 $\phi_{\text {start}}$ 是 cnf 形式。公式 $\phi_{\text {accept}}$ 是变量的大 OR,因此是一个单一子句。公式 $\phi_{\text {move}}$ 是唯一一个尚未采用 cnf 形式的公式,但我们可以很容易地将其转换为 cnf 形式的公式,如下所示。
回想一下,$\phi_{\text {move}}$ 是子公式的大 AND,每个子公式都是 OR 的 AND,描述所有可能的合法窗口。第0章中描述的分配律指出,我们可以用等价的 OR 的 AND 替换 AND 的 OR。这样做可能会显著增加每个子公式的大小,但它只能将 $\phi_{\text {move}}$ 的总大小增加一个常数因子,因为每个子公式的大小仅取决于 $N$。结果是一个合取范式的公式。
现在我们已经用 cnf 编写了公式,我们将其转换为每个子句包含三个文字的公式。在每个当前包含一个或两个文字的子句中,我们复制其中一个文字,直到总数为三个。在每个包含超过三个文字的子句中,我们将其分成几个子句,并添加额外的变量以保留原始子句的可满足性或不可满足性。
例如,我们将子句 $\left(a_{1} \vee a_{2} \vee a_{3} \vee a_{4}\right)$(其中每个 $a_{i}$ 都是一个文字)替换为两子句表达式 $\left(a_{1} \vee a_{2} \vee z\right) \wedge\left(\bar{z} \vee a_{3} \vee a_{4}\right)$,其中 $z$ 是一个新变量。
顶点覆盖问题
如果 $G$ 是一个无向图,则 $G$ 的顶点覆盖是节点的一个子集,其中 $G$ 的每条边都接触这些节点中的一个。顶点覆盖问题询问一个图是否包含指定大小的顶点覆盖:
VERTEX-COVER $=\{\langle G, k\rangle \mid G$ 是一个具有 $k$ 个节点顶点覆盖的无向图$\}$。
定理 7.44
VERTEX-COVER 是NP-完全的。
证明思路 为了证明 VERTEX-COVER 是NP-完全的,我们必须证明它在 NP 中,并且所有 NP 问题都可以多项式时间归约到它。第一部分很容易;证书就是大小为 $k$ 的顶点覆盖。为了证明第二部分,我们证明 3SAT 可多项式时间归约到 VERTEX-COVER。该归约将 3cnf-公式 $\phi$ 转换为一个图 $G$ 和一个数字 $k$,使得当 $G$ 具有 $k$ 个节点的顶点覆盖时,$\phi$ 是可满足的。转换是在不知道 $\phi$ 是否可满足的情况下完成的。实际上,$G$ 模拟 $\phi$。该图包含模拟公式的变量和子句的小工具。设计这些小工具需要一些独创性。
对于变量小工具,我们在 $G$ 中寻找一种结构,它可以以两种可能的方式参与顶点覆盖,对应于对变量的两种可能的真值赋值。变量小工具包含两个由边连接的节点。这种结构有效,因为其中一个节点必须出现在顶点覆盖中。我们任意将 TRUE 和 FALSE 与这两个节点关联起来。
对于子句小工具,我们寻找一种结构,它促使顶点覆盖包含变量小工具中对应于子句中至少一个真文字的节点。该小工具包含三个节点和额外的边,使得任何顶点覆盖都必须包含至少两个节点,或者可能全部三个。如果一个变量小工具节点通过覆盖一条边提供帮助,则只需要两个节点,就像相关文字满足该子句时发生的情况。否则,将需要三个节点。最后,我们选择 $k$,使得所寻求的顶点覆盖每个变量小工具有一个节点,每个子句小工具有两个节点。
证明 以下是 3SAT 到 VERTEX-COVER 的多项式时间归约的详细信息。该归约将布尔公式 $\phi$ 映射到图 $G$ 和值 $k$。对于 $\phi$ 中的每个变量 $x$,我们生成一条连接两个节点的边。我们用 $x$ 和 $\bar{x}$ 标记该小工具中的两个节点。将 $x$ 设置为真对应于选择标记为 $x$ 的节点作为顶点覆盖,而 FALSE 对应于标记为 $\bar{x}$ 的节点。
变量。如果 $a_{i}$ 的某些设置满足原始子句,我们可以找到 $z$ 的某些设置,使得两个新子句被满足,反之亦然。通常,如果子句包含 $l$ 个文字,
我们可以用 $l-2$ 个子句替换它
我们可以很容易地验证新公式是可满足的当且仅当原始公式是可满足的,所以证明完成。