1内容
好的,我将严格按照 解释工作流WorkFlow.md 的要求,对您提供的 Lec01-Numbers-260122打印1.ZH.md 文件内容进行逐段、逐句、逐细节的超详细解释。
我将确保:
- 不遗漏任何内容:从头到尾覆盖所有文本、标题、公式和图片。
- 严格遵循结构:使用 [原文]、[逐步解释]、[公式与符号逐项拆解和推导]、[具体数值示例]、[易错点与边界情况]、[总结]、[存在目的]、[直觉心智模型] 和 [直观想象] 的结构。
- 重新编号标题:使用带层级结构的自增数字替换原有标题。
- 详细解释:解释内容将远超原文长度,包含背景、概念拆解、示例、心智模型等。
- 公式处理:所有行间公式将被完整包含,并在文末提供带编号和解释的“行间公式索引”。
- 一次性输出:所有内容将在一个回复中完整提供,不会截断或省略。
现在开始生成解释内容。
2CSEE 3827:计算机系统基础(2026 年春季学期)- 详细解释
31. 课程与教师信息
📜 [原文1]
1CSEE 3827:计算机系统基础(2026 年春季学期)
1. 第 1 讲
授课教师:Dan Rubenstein 教授
电子邮箱:danr @cs.columbia.edu
这部分是课程讲义的封面页或起始页,提供了最核心的背景信息,明确了课程的身份、时间、主题以及负责人。
- CSEE 3827:这是课程的官方编号。在哥伦比亚大学(Columbia University)的课程体系中,这个编号具有唯一性,用于学生注册、成绩管理和学术记录。
- CSEE 是 "Computer Science and Electrical Engineering" 的缩写,表明这门课隶属于计算机科学与电气工程系。这是一个交叉领域的学科。
- 3827 是课程的数字代码。通常,3xxx 级别的课程是为本科高年级学生设计的,意味着它具有一定的深度和前置知识要求(尽管这门课叫“基础”)。
- 计算机系统基础:这是课程的正式名称。它揭示了课程的核心内容,即研究计算机是如何作为一个完整系统工作的。这里的“基础”指的是从最基本的数字逻辑和二进制运算开始,层层递进,最终构建起一个可编程的计算模型的宏伟蓝图。这门课不是教你如何使用某个软件,而是教你计算机本身是如何被设计和构建的。
- 2026 年春季学期:这明确了课程开设的具体时间。学术日历通常分为春季(Spring)和秋季(Fall)学期。
- 第 1 讲:这表明当前内容是本学期系列讲座中的第一讲,通常会包含课程介绍、管理性事务以及第一章的核心概念。
- 授课教师:Dan Rubenstein 教授:明确了教学负责人。Dan Rubenstein 是哥伦比亚大学计算机系的知名教授,他的研究领域通常涉及网络和系统。了解授课教师有助于学生查找其学术背景和过往的教学风格。
- 电子邮箱:danr @cs.columbia.edu:提供了教师的官方联系方式。这个邮箱地址是学生提问、提交作业(如果要求)或预约办公时间的重要渠道。@cs.columbia.edu 的域名后缀进一步确认了其在哥大计算机系的身份。邮箱地址中的空格 可能是为了防止网络爬虫自动抓取,实际发送邮件时需要去掉。
- 示例1(课程编号):如果你想在哥伦比亚大学的课程目录中查找这门课的信息,你会使用关键词 "CSEE 3827" 进行搜索,从而找到它的课程描述、先修课程要求、学分等信息。
- 示例2(联系教师):假设你对作业0的某个问题有疑问,你需要发送一封电子邮件。你应该将邮件发送到 danr@cs.columbia.edu(注意去掉了空格)。邮件主题可能是:“[CSEE 3827] Question about HW0”,正文中清晰地描述你的问题。
- 邮箱格式:最常见的错误是直接复制粘贴带空格的邮箱地址 danr @cs.columbia.edu,这会导致邮件发送失败。必须手动删除中间的空格。
- 课程编号混淆:学生有时会记错课程编号的后几位数字,例如记成 CSEE 3826 或 CSEE 3872,这会让他们找到错误的课程资料或教室。
- 讲次与日期:第 1 讲 不一定完全对应日历上的第一次课。有时第一次课可能完全用于课程介绍,而 第 1 讲 的学术内容从第二次课才开始。
本节是课程的身份标识,清晰地定义了课程代码、名称、学期、讲次以及授课教师和联系方式。它是所有后续内容的上下文基础。
这部分的存在是为了“确立身份和联系渠道”。它确保任何拿到这份讲义的人都能立刻知道这是什么课、谁在教、以及如何联系到负责人。这在学术环境中至关重要,是信息组织和沟通的起点。
可以把这部分想象成一本书的封面和扉页。封面告诉你书名(计算机系统基础)和作者(Dan Rubenstein 教授),扉页上则有出版信息(CSEE 3827, 2026年春季学期)和联系方式(电子邮箱)。你拿到任何一本书,第一眼看的就是这些信息,以确定它是不是你想要的,以及它的来源。
想象你走进一间大学教室,抬头看到投影屏幕上的第一张幻灯片。这张幻灯片上用大号字体写着课程名称、你的教授的名字以及他的邮箱。这就是这张讲义开头给你的感觉——一个清晰的、官方的开始。
42. 快速公告
📜 [原文2]
51. 快速公告
- 请填写办公时间可用性,链接如下:
- http://uribe.cs.columbia.edu/sched/table.php(截止日期:1 月 24 日,星期六)
- 作业 #0:可以先尝试!不要提交!解答将很快提供(可能在星期五)
这部分内容是课程开始时的“管理性事务”或“待办事项”,用于传达一些有时效性的重要信息,确保课程顺利运行。
- 办公时间 (Office Hours):这是教授和助教(TAs)每周专门留出的、用于学生前来提问和讨论的时间。为了让尽可能多的学生都能参加,教授需要收集学生们课余时间的空闲情况,从而安排一个最优的办公时间表。
- 填写可用性:这是一个需要学生主动完成的动作。教授提供了一个在线工具,让每个学生去标记自己哪些时间段有空。
- 链接:http://uribe.cs.columbia.edu/sched/table.php 是一个具体的网址。uribe.cs.columbia.edu 是哥大计算机系内部使用的一个服务器或工具平台。sched/table.php 指向一个用于安排(schedule)的表格(table)应用,这是一个动态网页(由PHP生成)。学生需要访问这个链接来完成上述的“填写可用性”任务。
- 截止日期:1 月 24 日,星期六。这是一个硬性deadline。教授需要在这个日期之后汇总所有学生的反馈,以便在下周初公布最终的办公时间安排。强调截止日期是为了确保学生不会错过,从而影响自己的权益。
- 作业 #0 (Homework #0):这是第一次作业,但编号为0,这通常暗示它是一次“热身”或“诊断性”作业。
- 可以先尝试!:鼓励学生主动去做。这通常是为了让学生评估自己对先修知识的掌握程度,或者提前熟悉课程的难度和题型。
- 不要提交!:明确指出这次作业不计入最终成绩,学生做完后不需要上交。这减轻了学生的压力,让他们可以更放松地去尝试和学习,而不是为了分数而做题。
- 解答将很快提供:教授会很快公布标准答案。这使得作业#0的主要目的变成了“自我检测”。学生可以通过对照答案,了解自己的不足之处,并知道应该在哪些方面投入更多精力。(可能在星期五) 提供了一个大致的时间预期。
- 示例1(填写办公时间):一个叫Alex的学生,他周一、周三的下午2点到4点没有课。他会登录那个.php链接,在一个类似日历的表格界面上,找到对应的时间格子并打上勾,表示他有空。教授的系统会收集到Alex以及其他所有同学的数据。
- 示例2(处理作业#0):一个叫Betty的学生下载了作业#0,发现里面有一些关于二进制和逻辑运算的问题。她花了一个小时做完了这些题。周五,教授把答案发了出来。Betty对照答案,发现自己错了一道关于二进制补码的题目。她意识到自己对这个概念的理解还不够扎实,于是她决定在第一讲(也就是本讲)之后,花更多时间复习这个知识点。她不需要担心这次错误会影响她的GPA,因为作业#0不提交也不计分。
- 错过截止日期:如果学生错过了 1月24日 这个截止日期,那么他在安排办公时间这件事上就失去了“投票权”。最终安排的时间可能正好与他的必修课冲突,导致他整个学期都很难参加办公时间。
- 误解作业#0的目的:如果一个学生不知道“不要提交”,他可能会花费大量时间去完美地完成并试图上传作业,结果做了无用功。更糟糕的是,如果他因为做作业#0而占用了学习其他计分内容的时间,就得不偿失了。
- 链接访问问题:uribe.cs.columbia.edu 这样的内部链接有时可能需要连接到学校的VPN才能访问。如果学生在校外直接点击链接打不开,可能会感到困惑。
本节是课程开始时的“行动号召”,包含两个紧急且重要的事项:一是要求学生在截止日期前提交自己的空闲时间以安排答疑,二是告知学生如何正确对待第一次非计分的热身作业。
这部分的存在是为了处理课程的行政和后勤工作,确保教学资源(如办公时间)能够有效配置,并引导学生以正确的方式开始新学期的学习。它将“程序性”信息与学术内容分开,使得开场白清晰高效。
可以把这部分想象成公司开周会时,项目经理在进入正题前说的几句开场白:“各位,在我们讨论项目进展之前,有两件事提醒一下:第一,下周团建的意向表今天下班前填完;第二,上周的培训材料发给大家了,可以自己看看,不用交学习报告。” 这都是为了让团队协作更顺畅的“润滑剂”。
想象教授站在讲台上,微笑着对大家说:“欢迎大家来上课!在我们正式开始之前,有两件小事需要大家配合一下。第一,请大家拿出手机或电脑,打开这个链接,花一分钟时间勾选一下你们下周的空闲时段,这周六之前完成哦。第二,课程网站上已经上传了‘作业0’,大家可以去练练手,找找感觉,不用交,我们周五会给答案。” 这种口头通知的感觉,被转化为了讲义上简洁的文字。
63. 关于讲义的说明
📜 [原文3]
72. 关于讲义的说明
- 本学期共有 13 份讲义
- 它们按主题分组
- 显然,我们不可能总是在一堂课中完成一套讲义。有些可能需要 2、3 或 4 次课堂讲座
这部分内容是对课程材料组织方式的解释,旨在管理学生的预期,让他们了解整个学期内容的结构和节奏。
- 本学期共有 13 份讲义:首先给出了一个明确的总量。学生可以预期整个学期会接触到 13 个主要的知识模块。这个数字帮助学生建立一个整体的学习地图,知道总共有多少“关卡”需要通过。
- 它们按主题分组:这解释了讲义的组织原则。每一份讲义(例如 Lec01-Numbers.pdf)都围绕一个特定的主题(例如数字系统)。这意味着内容不是按时间流水账组织的,而是按逻辑和知识依赖关系组织的。这是一种更有效的学习方式,有助于学生形成结构化的知识体系。
- 显然,我们不可能总是在一堂课中完成一套讲义:这是在管理学生的学习节奏预期。教授明确指出,一份讲义的内容量和一堂课(比如75分钟或90分钟)的时间是不严格对应的。
- 显然 (Obviously) 这个词暗示这是一个常识,或者说在大学课程中很常见。
- 这个说明打破了“一节课一份PPT”的中学或培训班模式。
- 有些可能需要 2、3 或 4 次课堂讲座:这给出了更具体的量化预期。一份内容丰富或难度较高的讲义,可能会分散在几周的课程中讲解。
- 例如,关于 CPU 设计的讲义,可能需要第一节课讲数据通路,第二节课讲控制逻辑,第三节课讲流水线。这三节课都会使用同一份讲义文件。
- 示例1:本讲(第1讲)的讲义是《Lec01-Numbers》,主题是数字系统。这部分内容相对基础,可能只需要1.5次课就能讲完。那么在第二次课的后半部分,教授就会开始讲《Lec02》的内容。
- 示例2:到了学期中段,可能会有一份名为《Lec07-Processor-Design》的讲义。这个主题非常复杂,包含了数据通路、控制单元、异常处理等多个子话题。教授可能会用第10、11、12、13次,总共4次讲座,才完整地讲解完这份讲义。在这期间,学生需要持续复习《Lec07》的内容。
- 错误的预期:如果学生没注意这个说明,他可能会以为每次上课都会从一份全新的讲义开始。当他发现教授还在讲上周的讲义时,他可能会感到困惑,甚至以为自己进错了教室或下载错了文件。
- 复习范围的误判:在准备期中考试时,学生不能简单地认为“考前5次课就考前5份讲义”。他们需要根据教授的实际授课进度,来确定考试覆盖了哪些讲义的哪些部分。可能前5次课只讲完了3份讲义。
- 讲义之间的关系:虽然讲义按主题分组,但主题之间是有强依赖关系的。学生不能因为某份讲义讲了很久就觉得它孤立,实际上,它是后续所有讲义的基础。
本节向学生说明了课程讲义的组织形式(13个按主题划分的模块)和授课节奏(一份讲义可能持续数周),旨在帮助学生建立正确的学习预期,合理安排复习计划。
这部分的存在是为了“设定预期,避免混淆”。它提前告知学生课程内容的宏观结构和微观节奏,防止学生因“讲义进度与课程次数不匹配”而产生困惑,从而能更专注于内容本身,而不是形式。
这就像你在看一部有13章的美剧。每一章(讲义)都讲述一个相对完整的故事(主题)。但是,导演(教授)并不会严格地在一集(一堂课)里讲完一章。有些简单的章节可能半集就讲完了,而一些复杂的章节(比如季中大高潮)可能要花整整三集的时间来铺垫、展开和收尾。你需要跟着导演的节奏走,而不是自己想象“一集就该有一章”。
想象你在玩一个有13个大关卡的游戏。每个关卡(讲义)都有一个独特的主题,比如“熔岩世界”、“冰雪迷宫”等。游戏设计师(教授)告诉你:“我们总共有13个大关。但请注意,不是你每次玩游戏都能通一关。有些小关卡你可能10分钟就过了,但像‘最终Boss城堡’这样的大关,你可能需要花好几天、反复尝试才能通过。” 这让你对整个游戏过程的耗时和难度分布有了心理准备。
84. 议程
📜 [原文4]
93. 议程 (M&K 章节 1, 3.11, 9.7)
- 从(非常高层次)数字视角看计算机
- 数字/二进制
- 与十进制、十六进制
- 术语:
- 位/字节/字 & 字长
- 最高有效位 (most significant) 位,最低有效位 (least significant) 位
- 负数格式:
- 符号/幅度
- 1 的补码
- 2 的补码
- 通过二进制的浮点 (P&H 3.5 - 跳过 MIPS 子节中的 FP)
- 加法
- 乘法
“议程”(Agenda)部分是本讲(Lec01)内容的详细路线图,列出了将要讨论的所有知识点。
- M&K 章节 1, 3.11, 9.7:这指向了课程使用的教科书。M&K 很可能是作者姓氏的缩写,一本经典的计算机系统教材是 Morris Mano 和 Charles Kime 合著的《Logic and Computer Design Fundamentals》。这部分告诉学生,本讲内容对应教科书的哪些章节,方便学生预习和复习。
- 从(非常高层次)数字视角看计算机:这是本讲的开篇立意。我们不直接深入复杂的电路,而是站在一个很高的抽象层次上,把计算机看作一个处理数字(特别是二进制数字)的机器。这是理解计算机工作原理的入口。
- 数字/二进制:核心概念,即计算机世界的基础语言是二进制,只有0和1。
- 与十进制、十六进制:讨论不同进制之间的关系和转换。十进制是人类习惯的,二进制是机器使用的,而十六进制是程序员为了方便读写二进制而使用的一种简写形式。
- 术语:接下来是一系列基础名词的定义。
- 位 (Bit):二进制数的一个位,是信息的最小单位。
- 字节 (Byte):8个位的组合,是内存和存储的基本单位。
- 字 (Word) & 字长 (Word Length):一个字是计算机一次能处理的位数,这个数量就是字长。例如,一个64位处理器,其字长就是64位。
- 最高有效位 (Most Significant Bit, MSB) 和 最低有效位 (Least Significant Bit, LSB):在一个二进制数中,最左边的位(权重最大)是MSB,最右边的位(权重最小)是LSB。
- 负数格式:在固定字长的二进制世界里,如何表示负数是一个关键问题。这里列出了三种主要的表示法:
- 符号/幅度 (Sign/Magnitude):最直观的方法,用一位表示符号(0为正,1为负),其余位表示绝对值大小。
- 1的补码 (1's Complement):一种求相反数的方法,通过将所有位取反得到。
- 2的补码 (2's Complement):现代计算机最普遍使用的方法,在1的补码基础上加1。它的加减法运算可以统一处理。
- 通过二进制的浮点 (Floating Point):如何用二进制表示小数(如3.14)和科学记数法(如 $6.02 \times 10^{23}$)。
- P&H 3.5:这指向了另一本可能的教科书,P&H 通常指 David Patterson 和 John Hennessy 的《Computer Organization and Design》。这说明浮点数部分参考了这本书的3.5节。
- 跳过 MIPS 子节中的 FP:这是一个重要的提醒。P&H的书中大量使用MIPS这一具体的指令集架构作为例子。教授在此特别指出,我们只学习浮点数的一般原理,而不需要深入研究它在MIPS架构上的具体实现细节(比如专用的浮点指令)。
- 加法 / 乘法:在定义了数字表示法(特别是2的补码)之后,议程的最后部分是学习如何在二进制下执行基本的算术运算。
- 示例1(进制转换):十进制数 26,在二进制中是 11010,在十六进制中是 1A。本讲会教你如何进行这些转换。
- 示例2(2的补码):在一个4位的系统中,数字 3 表示为 0011。它的相反数 -3 如何用2的补码表示?首先,所有位取反(1的补码)得到 1100,然后加1,得到 1101。所以 1101 就代表 -3。
- 示例3 (MSB/LSB):对于二进制数 10110,MSB 是最左边的 1 (代表 $2^4=16$),LSB 是最右边的 0 (代表 $2^0=1$)。
- 教材版本:M&K 和 P&H 都有很多个版本,学生需要确认教授使用的是哪个版本,否则章节号可能对不上。
- MIPS 指令:学生可能会因为好奇或不小心而深入去研究 MIPS 的浮点指令,但这会耗费不必要的时间,因为考试和作业可能并不会涉及。
- 负数表示法的混淆:在学习初期,学生很容易将符号/幅度、1的补码和2的补码搞混,尤其是在计算一个负数的二进制表示时。例如,对于-5(4位),符号/幅度是 1101,1的补码是 1010,2的补码是 1011。
本节是本讲内容的“目录”和“学习指南”,它详细列出了从计算机的数字抽象,到不同进制的表示与转换,再到核心术语、负数与小数的表示法,最后到二进制算术运算的全部知识点。同时,它还指明了对应的教科书章节,方便学生参考。
这部分的存在是为了“提供清晰的学习路径”。它让学生在学习开始前就对本讲的知识体系有一个完整的概览,知道自己将要学什么、学习的顺序是什么、重点和难点在哪里。这有助于学生带着问题去听讲,提高学习效率。
这就像你要去一个陌生的城市旅行,在出发前看了一张旅游地图。地图上标记了你要去的几个主要景点(数字系统、负数表示、浮点数...),并规划好了建议的游览路线。地图上还标注了“游客中心”的位置(教科书章节),方便你随时查阅更详细的信息。这张地图让你对整个旅程心中有数,而不是盲目地乱逛。
想象你正在玩一个烹饪游戏,这一关的任务是做一道复杂的“二进制蛋糕”。屏幕上显示出本关的“食谱”(议程):
- 准备基本食材:面粉(十进制)、鸡蛋(二进制)、巧克力(十六进制)。
- 学习专业术语:什么是“一撮盐”(位)、“一茶匙糖”(字节)。
- 处理特殊食材:如何制作“无糖奶油”(负数)和“水果夹心”(浮点数)。
- 开始烘焙:学习“混合”(加法)和“装饰”(乘法)的技巧。
这个食谱让你清楚地知道制作这个蛋糕的每一步,以及它们的先后顺序。
105. 课程概述:构建计算机(数字视角)
15.1. 课程概述:构建计算机(数字视角)原文与解释
📜 [原文5]
114. 课程概述:构建计算机(数字视角)
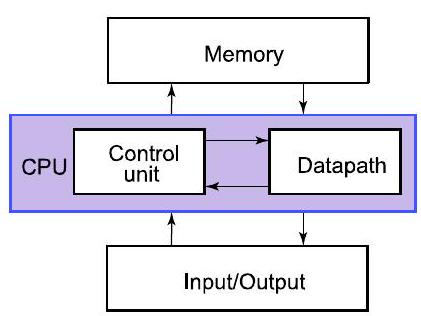
- CPU:计算机的“大脑”
- 控制单元对数据通路中的数据进行计算
- 内存:存储数据(供以后使用)
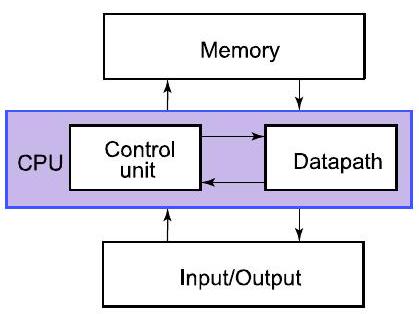
- 输入/输出:与外部的接口(磁盘、网络、显示器、键盘、鼠标等)
- 课程:从这种更简单的视图(下一幻灯片)开始
这部分内容从一个非常高的层次上介绍了计算机的经典体系结构,即冯·诺依曼结构的核心组件,并预告了本课程将如何逐步深入这些组件。
- CPU (Central Processing Unit):中央处理单元,被比喻为计算机的“大脑”。这是执行计算和决策的核心。
- 控制单元 (Control Unit):是CPU的“神经中枢”,负责指挥和协调。它会读取指令,解释指令,然后发出控制信号给其他部件。
- 数据通路 (Datapath):是CPU中实际执行数据处理的部分,像是“小脑”和“四肢”。它包含寄存器(用于临时存储数据)和算术逻辑单元(ALU)(用于执行加减乘除、与或非等运算)。控制单元发号施令,数据通路干活。
- 内存 (Memory):计算机的“记忆”。它用于存储程序指令和需要处理的数据。CPU需要计算时,就从内存中读取指令和数据;计算完成后,再把结果写回内存。这是一种易失性存储,断电后信息会丢失。
- 输入/输出 (Input/Output, I/O):这是计算机与外部世界沟通的桥梁。
- 输入设备:将外部信息传入计算机。例如,键盘和鼠标将你的操作转换为数字信号,磁盘和网络将文件和数据包读入内存。
- 输出设备:将计算机处理的结果呈现给外部世界。例如,显示器将图像数据显示出来,网络将数据包发送出去,磁盘将结果永久保存。
- 图片分析:
- 第一张图 f0fed655...-01.jpg 展示了 CPU 内部的简化模型,控制单元(Control)像一个指挥官,向数据通路(Datapath)发号施令。
- 第二张图 f0fed655...-02.jpg 展示了经典的计算机五大组成部分:控制器(Control)、运算器(Datapath)(这两者共同构成CPU)、存储器(Memory)、输入设备(Input) 和 输出设备(Output)。箭头表示了数据流(粗线)和控制流(细线)的方向。
- 课程:从这种更简单的视图(下一幻灯片)开始:这是一个重要的承上启下。教授在这里展示了完整的、复杂的计算机模型,但马上告诉学生:“我们不会一开始就啃这块硬骨头。” 课程将会从一个被极度简化的模型开始,然后逐步增加复杂性,最终再回到这个完整的模型。这是一种非常有效的教学策略。
- 示例1 (CPU工作流程):你想计算 3 + 5。
- 输入:你通过键盘输入 3 + 5。
- 内存:这个计算指令和数字 3、5 被加载到内存中。
- CPU:
- 控制单元从内存中读取“加法”指令。
- 控制单元命令数据通路从内存中取出 3 和 5。
- 数据通路中的ALU执行加法操作,得到 8。
- 控制单元命令数据通路将结果 8 存回内存。
- 输出:控制单元命令将结果 8 从内存送到显示器,你就在屏幕上看到了答案。
- 示例2 (I/O设备):你正在打一个网络游戏。你的鼠标点击和键盘敲击是输入。游戏程序(在CPU和内存中运行)根据你的输入计算出你的角色移动,然后通过显示器(输出)画出来。同时,你的移动信息通过网络(输出)发送到游戏服务器,服务器再把其他玩家的位置信息通过网络(输入)传回你的电脑。
- CPU与内存的关系:初学者容易认为CPU里面有巨大的存储空间。实际上,CPU内部只有非常少量、速度极快的寄存器用于临时周转。绝大部分数据都存放在外部的内存(RAM)中,CPU需要通过总线去读取。
- 内存与磁盘的区别:内存(RAM)是“短期记忆”,速度快但断电即忘。磁盘(硬盘/SSD)是“长期记忆”,速度慢但可以永久保存。操作系统和正在运行的程序放在内存里,而你的文件、照片、游戏安装包则放在磁盘里。
- 数据通路和控制单元:这两个概念非常抽象,很容易混淆。可以记住一个简单的比喻:控制单元是“工头”,只动嘴发指令;数据通路是“工人”,负责搬运(加载/存储)和加工(计算)数据。
本节通过经典的计算机五大部件模型(控制器、运算器、存储器、输入、输出),为学生描绘了一幅计算机系统的高层架构图。它定义了各个核心组件的职能,并预告了本课程将采用“从简到繁”的教学方法来逐一解析这些组件。
这部分的存在是为了“建立宏观认知框架”。在深入任何细节之前,先给学生一个计算机的全貌图景。这就像拼图一样,先看一下完整的封面图,再开始拼每一块,你就知道每一块大致应该放在哪里。
可以把计算机想象成一个高度自动化的大厨师(CPU)。
- 菜谱(程序)和食材(数据)都放在一个大冰箱(内存)里。
- 大厨师有一个大脑(控制单元),他会看菜谱,决定下一步是该切菜还是该开火。
- 他有一双巧手和一个料理台(数据通路),用来真正地切菜、炒菜。
- 采购员不断从市场上(输入设备,如网络、磁盘)把新食材放进冰箱。
- 服务员不断地把做好的菜(输出)端给客人(输出设备,如显示器)。
想象一下你面前有一个巨大的、透明的工厂模型。中间是核心的加工车间(CPU),里面有一个穿着白大褂、拿着指令板的经理(控制单元)在指挥,工人们(数据通路)在流水线上忙碌地操作机器。旁边是一个巨大的自动化立体仓库(内存),原材料和半成品在这里进进出出。工厂的一端是进货口(输入),卡车不断卸货;另一端是出货口(输出),成品被打包运走。这一整套联动的系统,就是计算机的直观模型。
15.2. 课程概述:第一季度
📜 [原文6]
24.1 课程概述:第一季度
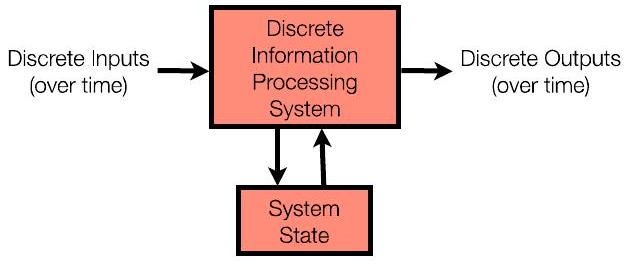
- 课程第一季度:非常简单的视图:“计算机”不维护状态
- 输入 → 计算 → 输出(仅仅是数学函数)
- 输入相同,输出相同
这是对课程第一阶段(约前1/4学期)学习内容的抽象和简化,定义了学习的起点。
- 非常简单的视图:教授再次强调,我们从一个极度简化的模型开始。
- 图片分析:图中展示了一个只有输入(Inputs)、计算(Computation)和输出(Outputs)的黑盒子。与上一页完整的计算机模型相比,这个模型砍掉了内存(Memory)和控制单元(Control)的复杂反馈循环。它就是一个纯粹的“计算器”。
- “计算机”不维护状态:这是对这个简化模型最核心的定义。“状态(State)”在这里指的是内存中存储的信息,也就是“记忆”。一个没有状态的系统,意味着它没有记忆能力。它无法记住上一次计算的结果,也无法根据历史输入来改变当前的行为。
- 输入 → 计算 → 输出(仅仅是数学函数):这个流程描述了这种无状态系统的工作模式。它像一个纯粹的数学函数 f(x)。你给它一个输入 x(Input),它通过内部的计算 f(Computation)逻辑,立即产生一个输出 y(Output)。整个过程是单向的、一次性的。
- 输入相同,输出相同:这是无状态系统(或纯函数)的一个关键特性,称为“幂等性”或“确定性”。无论你何时、何地、以何种顺序调用它,只要你给它的输入是相同的,它返回的输出就必须是相同的。例如,一个计算平方的函数,输入是4,输出永远是16。
这个阶段学习的主要是组合逻辑电路 (Combinational Logic Circuits)。这类电路的输出仅由当前的输入决定,没有任何记忆功能。
- 示例1(加法器):一个简单的2位加法器。
- 输入:两个2位的二进制数,例如 A=01 (1) 和 B=10 (2)。
- 计算:电路内部的逻辑门(与门、或门、异或门)执行二进制加法。
- 输出:一个3位的结果 S=011 (3)。
- 如果你再次输入 A=01 和 B=10,输出必然还是 011。它不会记得你上一次算过,也不会因此改变行为。
- 示例2(计算器上的 sin 函数):你按 sin(30),计算器显示 0.5。你再按一次 sin(30),它还是显示 0.5。这个 sin 按钮背后的逻辑就是一个无状态的计算单元。它不关心你之前算过什么。
- 与真实计算机混淆:学生可能会觉得这个模型太简单了,以至于不像一个“计算机”。需要明确这只是学习的第一步。真实计算机的核心优势恰恰在于其有状态(能存储程序和数据)。
- “状态”的理解:初学者可能不理解什么是“状态”。可以解释为“上下文”、“记忆”或“历史记录”。一个没有状态的系统是“健忘的”,它的每一次操作都是独立的。
课程的第一阶段将从一个最简化的计算机模型——无状态的组合逻辑系统——入手。这个系统像一个纯数学函数,其输出完全由当前输入决定,没有任何记忆功能。这个特性表现为“输入相同,输出相同”。
这部分的存在是为了“降低入门门槛,聚焦核心计算”。通过暂时剥离复杂的内存和状态管理,学生可以专注于最核心的“计算”本身是如何用数字逻辑实现的。学完这部分,学生将能搭建出任何可以被描述为数学函数的计算模块,为后续构建更复杂的系统打下坚实基础。
这就像学习开车时,教练让你先在驾校的模拟器上练习。这个模拟器(第一季度的模型)只有方向盘(输入)、油门刹车(输入)和屏幕上的画面(输出)。你转方向盘,车就转弯。它没有复杂的交通状况,没有GPS导航历史(内存),也没有自动驾驶系统(控制单元)。你只需要学习最基本的“输入如何直接导致输出”的对应关系。
想象一个老式的自动售货机。
- 输入:你投入一枚硬币(比如1元)。
- 计算:机器内部的机械结构检测到是1元硬币。
- 输出:它“咔嚓”一声掉下一瓶可乐。
这个过程是固定的。你每次投1元,它就掉一瓶可乐。它不记得你买过多少瓶,也不会因为你买得多就给你打折。这就是一个简单的输入→计算→输出的无状态系统。
35.3. 课程概述:第二季度
📜 [原文7]
44.2 课程概述:第二季度
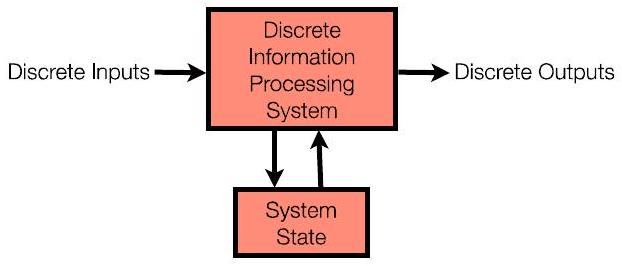
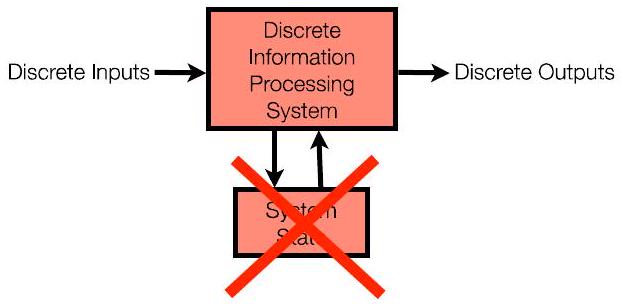
- 第二季度:“计算机”有内存(系统状态)
- 可以使用输入和内存中存储的内容来确定输出
这是对课程第二阶段(约第二个1/4学期)学习内容的介绍,标志着模型复杂度的第一次跃升。
- 图片分析:与第一季度的图相比,这张图的核心变化是增加了一个“内存 (Memory)”或“状态 (State)”模块。并且,计算 (Computation) 单元不仅接收外部输入 (Inputs),还从内存中读取数据。同时,计算单元的输出 (Outputs) 不仅流向外部,还会有一路返回去更新内存中的内容。这就形成了一个反馈循环 (feedback loop)。
- “计算机”有内存(系统状态):这是与第一阶段最本质的区别。我们的模型从“健忘的”纯函数,进化成了“有记忆的”机器。它引入了状态,即可以保存信息供以后使用。
- 可以使用输入和内存中存储的内容来确定输出:这描述了有状态系统的工作方式。输出不再仅仅取决于当前的输入,而是由 当前输入 和 当前内存中的状态 共同决定。用函数来表示,就是 Output = f(Input, State)。
- 由于计算结果可以反过来更新状态 (New_State = g(Input, State)),这意味着系统的行为会随着时间演变。相同的输入在不同时间点可能会产生不同的输出,因为系统的“记忆”或状态已经改变了。
这个阶段学习的主要是时序逻辑电路 (Sequential Logic Circuits)。这类电路(如锁存器、触发器、寄存器、计数器)包含存储元件,它们的输出取决于当前输入和电路的历史状态。
- 示例1(计数器):一个简单的加1计数器。
- 状态:内存中存储着当前计数值,比如是 5。
- 输入:一个“加1”的信号(比如你按了一下按钮)。
- 计算:电路读取当前状态 5 和“加1”输入,计算出 5 + 1 = 6。
- 输出:它将 6 显示出来。
- 状态更新:同时,它用新的值 6 去更新内存中的状态。
- 下一次你再给一个“加1”的输入,它读取的状态已经是 6,所以输出会是 7。可见,相同的输入(“加1”信号)导致了不同的输出(先是6,后是7)。
- 示例2(银行ATM):
- 状态:你的账户余额,比如是 1000 元。
- 输入:你插入银行卡,选择“取款 200 元”。
- 计算:ATM系统读取你的余额 1000 和取款额 200,确认 1000 >= 200。
- 输出:吐出 200 元现金。
- 状态更新:系统将你的账户余额更新为 1000 - 200 = 800 元。
- 如果你再次输入“取款 900 元”,系统会读取新余额 800,发现 800 < 900,于是输出“余额不足”的提示。相同的取款操作,因为状态(余额)不同,行为也不同。
- 反馈循环的理解:这个模型的核心是反馈循环。学生需要理解,正是因为输出可以影响未来的状态,才使得系统具有了“行为”和“历史”。
- 时钟信号:在实际的时序逻辑中,状态的更新不是瞬间发生的,而是由一个全局的“时钟”信号同步的。讲义在这里为了简化没有画出时钟,但在后续学习中这是至关重要的概念。
课程的第二阶段在第一阶段的无状态模型基础上,引入了内存(状态)。这使得计算机模型从一个简单的计算器进化成一个能记忆、能演化的系统。它的输出由当前输入和历史状态共同决定,并且其计算结果可以反过来更新自身状态,为更复杂的计算(如执行程序)铺平了道路。
这部分的存在是为了“引入‘记忆’的概念”。这是从纯粹的组合逻辑迈向真正的计算机的关键一步。有了状态,我们才能构建存储器、寄存器,并最终搭建出一个可以加载并执行指令序列的处理器。
这就像你从使用模拟器毕业,开始上路练车了。现在的系统(第二季度的模型)不仅有方向盘和油门(输入),还有了真实的道路环境和GPS导航(状态)。你当前应该左转还是右转(输出),不仅取决于你打了多少方向盘(输入),还取决于你当前在城市的哪个位置(状态)。你每开过一个路口,你的位置(状态)就会更新,GPS会给你新的指示。
想象一个有记忆功能的智能售货机。
- 状态:它记得你的会员积分是 50分。
- 输入:你投入1元硬币。
- 计算:它检测到1元硬币,同时读取你的积分 50。
- 输出:它掉下一瓶可乐,并显示“积分+10”。
- 状态更新:它将你的积分更新为 50 + 10 = 60。
- 下次你再买东西,它就知道你的积分是从60分开始累加了。这个售货机的行为(累加积分)依赖于它的“记忆”。
55.4. 课程概述:后半部分
📜 [原文8]
64.3 课程概述:后半部分
计算机处理程序(存储在内存中)
- 程序由指令序列组成
- 程序修改也存储在内存中的数据
本学期稍后会详细介绍...
- 丹尼尔必须“打蜡,擦拭”才能掌握空手道..


- 你也必须“打蜡,擦拭”,然后我们才能进入更有趣的内容
到五月...

到五月...

到五月...


这部分内容描绘了课程后半段(第三、四季度的)的宏伟目标,并用一个生动的比喻来激励学生,说明前期基础知识的重要性。
- 计算机处理程序(存储在内存中):这是计算机区别于计算器的本质飞跃。我们不仅在内存中存数据,更重要的是,我们把操作数据的步骤——程序 (Program)——也存放在内存中。这就是著名的“存储程序”概念,是现代计算机的基石。
- 程序由指令序列组成:一个程序被分解成一系列非常简单的、机器可以理解的指令 (Instructions),比如“加载数据”、“相加”、“存储结果”、“跳转到另一条指令”等。CPU的工作就是一条一条地执行这些指令。
- 程序修改也存储在内存中的数据:这解释了程序的最终目的。程序通过执行指令序列,来读取、处理并修改同样存放在内存中的数据。整个计算过程,就是程序(一系列指令)在内存中对数据进行操作的过程。
- 图片分析 ...-02.jpg:这张图展示了一个处理器 (Processor) 与内存 (Memory) 的交互。内存中既有指令 (Instructions),也有数据 (Data)。处理器从内存中取出指令来执行,并根据指令的要求去读写内存中的数据。
接下来,教授用了一个非常经典的比喻:
- 本学期稍后会详细介绍...:再次明确,这是未来的内容,现在只是让你看一眼目标。
- 丹尼尔必须“打蜡,擦拭”才能掌握空手道..:这是一个文化引用,来自1984年的电影《龙威小子》(The Karate Kid)。影片中,空手道大师宫城先生 (Mr. Miyagi) 并没有直接教主角丹尼尔 (Daniel) 空手道招式,而是让他日复一日地做一些看似无关的杂活,比如给汽车打蜡(“wax on, wax off”)和擦地板。丹尼尔感到非常枯燥和不解,但后来发现,这些重复的动作已经训练了他的肌肉记忆和格斗的基本功。
- 图片分析 ...-03.jpg:展示了电影中丹尼尔在宫城先生指导下练习“打蜡,擦拭”的场景。
- 你也必须“打蜡,擦拭”,然后我们才能进入更有趣的内容:教授在这里将自己比作宫城先生,将学生比作丹尼尔。课程前期的组合逻辑(第一季度)和时序逻辑(第二季度)就像是“打蜡”和“擦拭”。这些内容可能看起来有些枯燥、琐碎、抽象,甚至让人觉得“这跟计算机有什么关系?”。但教授保证,这些是构建一个完整处理器的基本功。只有掌握了这些基础,才能理解和设计后半学期“更有趣的内容”——一个真正的、能执行程序的CPU。
- 到五月...:五月是春季学期的结束时间。教授用一系列越来越复杂、越来越酷炫的图片来展示学期末学生将达到的高度。
- 第一张 ...-03.jpg 动图可能展示了一个简单的逻辑电路模拟。
- 第二张 ...-03.jpg 动图可能是一个更复杂的、能执行简单指令的数据通路模拟。
- 第三张 ...-03.jpg 动图可能是一个完整的、带有控制单元和内存交互的处理器在运行程序。
- 最后的 ...-04.jpg 图片可能是一个真实CPU芯片的物理版图或者一个复杂系统运行的截图,象征着最终的成功。
- 示例1(程序与数据):假设内存地址100到102存放了程序:
- 100: LOAD A, 200 (从地址200加载数据到寄存器A)
- 101: ADD A, 201 (将地址201的数据与寄存器A相加)
- 102: STORE A, 202 (将结果存到地址202)
而地址200和201存放了数据:
- 200: 5
- 201: 10
CPU执行这个程序后,地址202的数据就会被修改为15。
- 示例2 (“打蜡”练习):学习如何用与门、或门、非门搭建一个全加器。这个过程可能很繁琐,需要画真值表、写逻辑表达式、化简。这就像“打蜡”。但只有掌握了如何搭建加法器,你才能在以后设计CPU的算术逻辑单元(ALU)时,知道如何实现加法功能。
- 失去耐心:学生在学习基础逻辑门和时序电路时,很容易因为看不到“大图景”而感到沮丧和失去动力。这个比喻正是为了解决这个问题,告诉学生要相信这个过程。
- 指令和数据的混淆:在冯·诺依曼架构中,指令和数据都以二进制形式存放在同一个内存中,本质上没有区别。这既是其优势(灵活性),也可能带来问题(例如,程序错误地将数据当作指令来执行,或修改了自身的指令)。
课程的后半部分将聚焦于最终目标:设计一个能够执行存储在内存中的程序的完整计算机系统。教授通过引用《龙威小子》中“打蜡,擦拭”的经典比喻,强调了前期基础知识(组合逻辑和时序逻辑)对于掌握后续高级内容(处理器设计)的决定性重要性,并用一系列激动人心的愿景图来激励学生坚持下去。
这部分的存在是为了“连接基础与目标,并提供情感激励”。它清晰地指出了课程的最终山顶在哪里(设计一个真正的处理器),同时告诉学生,通往山顶的路必须从山脚下最基础的台阶(逻辑电路)开始铺设。这个比喻能极大地激发学生的学习动力,帮助他们理解并忍耐前期的枯燥,为了最终的“有趣”而努力。
这就像学乐高。
- “打蜡,擦拭”:你正在学习认识各种最基本的积木块:2x2的、2x4的、带斜面的、带轮子的(组合逻辑、时序逻辑)。你还需要学习如何将它们稳固地拼在一起(逻辑门的组合)。这个过程可能很枯燥。
- “更有趣的内容”:课程后半段,老师会给你一张非常酷的“千年隼”号飞船的设计图(处理器架构)。因为你已经对所有基础积木和拼接技巧了如指掌,所以你现在可以看懂设计图,并亲手把成千上万个小积木块,搭建成那艘宏伟的飞船(一个能运行程序的CPU)。如果你之前没耐心学基础,现在面对一堆零件和复杂的设计图,只会一脸茫然。
想象你正在一个健身房里,教练(教授)对你说:
“我们的最终目标是让你能举起150公斤的杠铃(设计处理器)。”
“但在那之前,接下来的两个月(第一、二季度),你每天的训练就是俯卧撑、引体向上和深蹲(逻辑电路基础)。我知道这很无聊,但这是你核心力量的基础。相信我,等你核心力量上来了,我们再上大重量就会非常轻松和安全(进入更有趣的内容)。”
然后教练给你看墙上挂着的顶级举重运动员的照片(“到五月...”的图片),说:“到学期末,你也能像他们一样。”
126. 不同进制的加法
16.1. 数制回顾:10 进制 (十进制)
📜 [原文9]
135. 不同进制的加法
15.1 数制回顾:10 进制 (十进制)
- 人类(通常)处理数字的方式
- 10 个数字 $=\{0,1,2,3,4,5,6,7,8,9\}$
- 示例:4537.8 基数 10 又名 $(4537.8)_{10}$
这一节开始进入本讲的核心技术内容。它首先回顾我们最熟悉的十进制系统,以便与后续的二进制和十六进制进行对比。
- 人类(通常)处理数字的方式:开宗明义,十进制(Decimal, base-10)是我们日常生活中默认使用的计数系统。这源于人类有10个手指,方便计数。
- 10 个数字 = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}:十进制系统的基础是10个不同的符号(数码)。所有的十进制数都是由这10个符号组合而成的。
- 示例:4537.8 基数 10 又名 $(4537.8)_{10}$:这里给出了一个具体的例子。
- 4537.8 是数字的表示。
- 基数 10 或 ( ... )_{10} 是为了明确指出这个数是在十进制下表示的。在没有歧义的情况下,我们通常省略这个下标。基数 (Base/Radix) 指的是一个数制系统中使用的数码的个数,这里是10。
- 公式分析:这个部分用一种展开的形式,揭示了十进制的本质——它是一种按权展开的位置计数法。
- 位置计数法:同一个数码(如4)在不同的位置,其代表的值是不同的。
- 权 (Weight):每一个位置都有一个对应的权重,这个权重是基数的整数次幂。小数点左边,从右到左,权重依次是 $10^0, 10^1, 10^2, 10^3, \dots$。小数点右边,从左到右,权重依次是 $10^{-1}, 10^{-2}, \dots$。
- 一个数的值,等于它每一位上的数码乘以该位对应的权,然后将所有结果相加。
- 在例子 4537.8 中:
- 4 在千位上,值为 $4 \times 10^3 = 4000$。
- 5 在百位上,值为 $5 \times 10^2 = 500$。
- 3 在十位上,值为 $3 \times 10^1 = 30$。
- 7 在个位上,值为 $7 \times 10^0 = 7$。
- 8 在小数点后第一位,值为 $8 \times 10^{-1} = 0.8$。
- 将它们全部相加:$4000 + 500 + 30 + 7 + 0.8 = 4537.8$。
- 拆解:
- 这个表示法虽然不是一个严谨的数学公式,但它直观地展示了计算过程。
- 第一行 4 5 3 7 . 8 是原始数字的各位数码。
- 第二行 x 10^3, x 10^2, x 10^1, x 10^0, x 10^-1 是对应位置的权。
- 下面几行 4000, 500, 30, 7, 0.8 是每个数码乘以其权的结果。
- 最后的等式将所有这些结果加起来,得到最终的值。
- 通用推导:对于一个十进制数 $d_n d_{n-1} \dots d_1 d_0 . d_{-1} d_{-2} \dots d_{-m}$,其值为:
其中 $d_i$ 是在第 $i$ 位的数码(0-9之间)。对于 4537.8,这里 $n=3, m=1$,$d_3=4, d_2=5, d_1=3, d_0=7, d_{-1}=8$。
- 示例1(整数):数字 1024。
- $1 \times 10^3 + 0 \times 10^2 + 2 \times 10^1 + 4 \times 10^0$
- $= 1000 + 0 + 20 + 4$
- $= 1024$。
- 示例2(小数):数字 25.04。
- $2 \times 10^1 + 5 \times 10^0 + 0 \times 10^{-1} + 4 \times 10^{-2}$
- $= 20 + 5 + 0 + 0.04$
- $= 25.04$。
- 第0位:初学者容易忘记小数点左边第一位(个位)的权是 $10^0=1$,而不是 $10^1$。
- 小数位:小数点右边第一位的权是 $10^{-1}=0.1$,负指数在这里表示除法。
- 位的价值:向左移动一位,数字的值乘以10;向右移动一位,数字的值除以10。
本节通过回顾我们日常使用的十进制系统,重点复习了其作为“按权展开的位置计数法”的本质。一个十进制数的值,是其每一个数码与其所在位置的权(10的幂)相乘后求和的结果。这是理解其他进制(如二进制)的基础。
这部分的存在是为了“建立一个熟悉的参照系”。通过剖析人人皆知的十进制,引出“基数”、“数码”、“位置”和“权”这几个核心概念。有了这个共同的理解基础,接下来将这些概念应用到不熟悉的二进制和十六进制时,学生就能更容易地举一反三,理解其原理。
想象你手头有不同面值的纸币:1元、10元、100元、1000元。这些就是“权”。数字 4537 就相当于你有 4 张1000元,5 张100元,3 张10元,和 7 张1元。你的总财富就是把这些纸币的价值加起来。十进制的每一位,就像一个只能放0-9张纸币的格子,格子的位置决定了里面放的是哪种面值的纸币。
想象一个古老的算盘。算盘的每一档(位置)代表一个权(个、十、百、千...)。每一档上的算珠(数码)数量有限(比如上下各5个,代表0-9)。数字 4537 就是在“千”档拨 4 个珠子,在“百”档拨 5 个,在“十”档拨 3 个,在“个”档拨 7 个。整个算盘表示的数值,就是这些珠子代表的值的总和。
26.2. 数制回顾:10 进制 (十进制) - 重复内容
📜 [原文10]
35.1.1 数制回顾:10 进制 (十进制)
- 人类(通常)处理数字的方式
- 10 个数字 $=\{0,1,2,3,4,5,6,7,8,9\}$
- 示例:4537.8 基数 10 又名 $(4537.8)_{10}$
- 计算机如何“思考”数字
- 2 个数字 $=\{0,1\}$
- 示例:$(1011.1)_{2}$
这个小节在讲义中出现了重复的内容,它再次展示了十进制的回顾,并紧接着引入了二进制的初步介绍。我们将重点解释新引入的二进制部分。
- 计算机如何“思考”数字:与“人类处理数字的方式”相对应,这里点明了二进制 (Binary, base-2) 是计算机内部使用的语言。
- 2 个数字 = {0, 1}:二进制的基数是2,所以它只使用两个数码:0 和 1。这是因为计算机的底层硬件(晶体管)最容易实现和区分两种物理状态,例如高电平和低电平、开和关、有和无。
- 示例:$(1011.1)_{2}$:这是一个二进制数的例子。下标 2 明确了其基数。
- 公式分析:与十进制完全类似,二进制也是一种按权展开的位置计数法,唯一的区别是基数从10换成了2。
- 权 (Weight):每一个位置的权重是2的整数次幂。小数点左边,从右到左,权重依次是 $2^0, 2^1, 2^2, 2^3, \dots$。小数点右边,从左到右,权重依次是 $2^{-1}, 2^{-2}, \dots$。
- 对于例子 $(1011.1)_2$:
- 最左边的 1 在 $2^3$ 位上,值为 $1 \times 2^3 = 8$。
- 第二个 0 在 $2^2$ 位上,值为 $0 \times 2^2 = 0$。
- 第三个 1 在 $2^1$ 位上,值为 $1 \times 2^1 = 2$。
- 第四个 1 在 $2^0$ 位上,值为 $1 \times 2^0 = 1$。
- 小数点后的 1 在 $2^{-1}$ 位上,值为 $1 \times 2^{-1} = 0.5$。
- 将它们全部相加:$8 + 0 + 2 + 1 + 0.5 = 11.5$。
- 所以,二进制数 $(1011.1)_2$ 等价于十进制数 $(11.5)_{10}$。
- 第一个公式为重复的十进制内容,此处不再赘述。
- 第二个公式:
- 拆解:这个公式的排版有些混乱,但其意图是展示 $(1011.1)_2$ 的按权展开。
- 1 x 2^3 对应最左边的 1。
- 0 x 2^2 对应第二个 0(公式中省略了)。
- 1 x 2^1 对应第三个 1。
- 1 x 2^0 对应第四个 1。
- 1 x 2^-1 对应小数点后的 1。
- 其计算结果是:$8 + 0 + 2 + 1 + 0.5 = 11.5$。
- 最后的 =(11.5)_{10} 明确了转换后的结果是十进制的。
- 通用推导:对于一个二进制数 $b_n b_{n-1} \dots b_1 b_0 . b_{-1} b_{-2} \dots b_{-m}$,其值为:
其中 $b_i$ 是在第 $i$ 位的数码(0或1)。
- 示例1(二进制转十进制):二进制数 $(1101)_2$。
- $1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0$
- $= 8 + 4 + 0 + 1$
- $= (13)_{10}$。
- 示例2(带小数的二进制转十进制):二进制数 $(101.01)_2$。
- $1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 + 0 \times 2^{-1} + 1 \times 2^{-2}$
- $= 4 + 0 + 1 + 0 + 0.25$
- $= (5.25)_{10}$。
- 权重记忆:需要牢记2的幂次:$2^0=1, 2^1=2, 2^2=4, 2^3=8, 2^4=16, \dots$。这在手动转换时非常关键。
- 下标的重要性:在同时处理多种进制时,必须清晰地写出下标,如 $(101)_2$ 和 $(101)_{10}$ 是完全不同的两个数(二进制的5 vs 十进制的一百零一)。
本节在复习十进制之后,核心是引入了计算机使用的二进制系统。它解释了二进制同样遵循“按权展开的位置计数法”,只是基数为2,权是2的幂。通过一个例子演示了如何将一个二进制数转换为等价的十进制数。
这部分的存在是为了“完成从人类语言到机器语言的第一次过渡”。它利用学生刚刚在十进制上复习过的“按权展开”这一核心思想,将其平移到二进制上,使得二进制的理解变得自然而简单。这是整个课程的技术基石。
如果说十进制的钱币体系是 1元, 10元, 100元...,那么二进制的钱币体系就是 1元, 2元, 4元, 8元, 16元...。一个二进制数,比如 $(1011)_2$,就代表你是否拥有某种面值的钱币。
- 你有 1 枚8元硬币。
- 你 0 枚4元硬币。
- 你有 1 枚2元硬币。
- 你有 1 枚1元硬币。
你的总财富就是 $8+2+1=11$ 元。
想象一排电灯开关。每个开关只有两种状态:开(代表1)和关(代表0)。这一排开关就构成了一个二进制数。从右到左,每个开关的“价值”依次是1, 2, 4, 8, ...。如果一排开关的状态是“开、关、开、开”,就对应二进制数 1011。整个房间的“亮度”(总价值)就是 $8+0+2+1=11$。
46.3. 数制:2 进制 (二进制)
📜 [原文11]
55.2 数制:2 进制 (二进制)
- 计算机如何“思考”数字
- 2 个数字 $=\{0,1\}$:我们将二进制数字称为位
- 示例:$(1011.1)_{2}$
将一列向左移会使数字的值乘以 2
这一节是对上一小节二进制介绍的确认和补充,并引入了一个核心术语和一个重要性质。
- 计算机如何“思考”数字 / 2 个数字 = {0, 1} / 示例 / 公式:这部分内容与 5.1.1 节完全相同,再次强调了二进制是计算机的基础,其表示法遵循按权展开原则。
- 我们将二进制数字称为位 (bit):这是一个非常重要的术语定义。
- 位 (Bit) 是 "Binary Digit" 的缩写。
- 它是信息的最小、最基本的单位。一个位只能存储 0 或 1 两种状态之一。
- 计算机中所有更复杂的信息,如数字、字母、图片、声音,最终都是由大量的位序列组合而成的。
- 将一列向左移会使数字的值乘以 2:这是二进制数的一个根本性质,源于其基数为2。
- 在位置计数法中,某一位的权是其右边一位的基数倍。
- 对于二进制,左边一位的权是右边一位的 $2$ 倍 (例如,$2^3=8$ 是 $2^2=4$ 的两倍)。
- 因此,将一个二进制数的所有位向左移动一位(并在最右边补0),其效果等同于将这个数的值乘以2。这被称为逻辑左移 (Logical Left Shift)。
- 这个性质非常重要,因为在硬件层面,移位操作比乘法操作快得多、省电得多。因此,当需要乘以2的幂时,计算机通常会用移位操作来代替乘法。
本节的公式与 5.1.1 节相同,此处不再重复拆解。
- 示例1 (左移):
- 取一个二进制数 $(110)_2$,其十进制值为 $4+2 = 6$。
- 将其左移一位,得到 $(1100)_2$。
- 计算新数的值:$8+4 = 12$。
- 可以看到,$12 = 6 \times 2$。左移一位,值乘以2。
- 示例2 (右移):
- 取一个二进制数 $(1010)_2$,其十进制值为 $8+2=10$。
- 将其右移一位(逻辑右移,丢弃最右位,最左补0),得到 $(0101)_2$。
- 计算新数的值:$4+1=5$。
- 可以看到,$5 = 10 / 2$。右移一位,(对于偶数)值除以2。
- 移位与乘除法不等价的情况:对于奇数的右移,结果是向下取整的。例如,$(1101)_2 = 13$,右移一位是 $(0110)_2 = 6$,即 $\lfloor 13/2 \rfloor$。对于负数,移位操作(特别是右移)更为复杂,分为算术右移和逻辑右移,我们会在后面学到。
- 术语精度:位 (bit) 是单个二进制数字。8个位组成一个字节 (Byte)。不要将两者混淆。下载速度 100 Mbps (兆位/秒) 和文件大小 100 MB (兆字节) 是不同的,前者要除以8才约等于后者。
本节在重申二进制基本概念的同时,正式引入了核心术语“位 (bit)”,并揭示了二进制数的一个关键算术性质:逻辑左移一位等价于乘以2。这个性质在底层硬件优化中扮演着重要角色。
这部分的存在是为了“夯实基础并引入核心操作”。在理解了二进制的表示法之后,必须掌握它的基本单位“位”,并开始了解可以直接在二进制表示上进行的、有意义的算术操作(如移位)。这为后续学习二进制加法、乘法以及ALU设计埋下伏笔。
想象你在用二进制钱币体系 1, 2, 4, 8...。
- 左移操作:相当于你把你所有的钱币都换成面值大一倍的。你原来有 1 枚1元和 1 枚4元(共5元,即 (101)_2)。现在,教练把你这 2 枚钱币收走,换给你 1 枚2元和 1 枚8元(共10元,即 (1010)_2)。你的总财富乘以了2。
再次想象那排电灯开关(从右到左价值为1, 2, 4, 8...)。
- 假设当前状态是 ...0011 (3)。
- 现在,你把每个开关的状态传递给它左边的邻居:原来价值1的开关状态给了价值2的开关,原来价值2的开关状态给了价值4的开关... 并在最右边(价值1)关灯。
- 新状态变为 ...0110 (6)。
- 这个“状态向左传递”的物理过程,就直观地展示了左移操作如何使总价值翻倍。
66.4. 数制:16 进制 (十六进制)
📜 [原文12]
75.3 数制:16 进制 (十六进制)
- (书呆子)人类与计算机交互的方式
- 16 个数字 = \{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F\}
| 基数 16 (十六进制) 值 | 基数 2 (二进制) 值 | 基数 10 值 |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
这一节引入了第三种重要的数制——十六进制 (Hexadecimal, hex, base-16),并解释了它为何在计算机领域如此常用。
- (书呆子)人类与计算机交互的方式:这是一个有趣的说法。如果说十进制是普通人的语言,二进制是计算机的语言,那么十六进制就是介于两者之间的“程序员黑话”或“工程师速记”。它主要不是为了计算,而是为了更方便地阅读和书写计算机内部的二进制数据。
- 16 个数字 = {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}:十六进制的基数是16。因为它需要16个不同的符号,而阿拉伯数字只有10个(0-9),所以就借用了英文字母表的前6个字母 A, B, C, D, E, F 来分别代表十进制中的 10, 11, 12, 13, 14, 15。
- 表格分析:这张表格是理解和使用十六进制的关键,必须熟记。
- 它清晰地列出了十六进制数码、对应的4位二进制值,以及等价的十进制值。
- 核心关系:一个十六进制位正好可以表示16个不同的值(0-15)。而4个二进制位 ($2^4$) 也正好可以表示16个不同的值(0000到1111)。
- 正是因为 $16 = 2^4$ 这个完美的数学关系,使得十六进制和二进制之间的转换异常简单。一个十六进制位 恰好等价于 四个二进制位。这就是十六进制存在的根本原因。
- 示例1 (二进制转十六进制):
- 有一个二进制数 1101 0101。
- 将其从右到左,每4位分为一组:1101 和 0101。
- 查表可知:1101 对应 D,0101 对应 5。
- 所以,二进制数 11010101 就是十六进制数 D5。
- 示例2 (十六进制转二进制):
- 有一个十六进制数 4C。
- 查表可知:4 对应 0100,C 对应 1100。
- 将它们拼接起来,得到二进制数 0100 1100。
- 示例3 (为何不用其他进制):为什么不用八进制 (Octal, base-8)?八进制也和二进制有类似关系 ($8=2^3$),一个八进制位对应三个二进制位。在早期计算机(如12位、36位系统)中八进制很常用。但在现代以8位(字节)为基本单位的计算机中,一个字节(8位)可以完美地由两个十六进制位表示,而八进制则需要 2 又 2/3 个位,非常不整齐。因此,十六进制胜出。
- 字母大小写:在表示十六进制数时,字母 A-F 通常不区分大小写。例如,0xAF 和 0xaf 是等价的。
- 与十进制的混淆:看到 10,在十进制下是十,但在十六进制下是十六(十进制的16)。看到 A,不能按字母表顺序想当然,必须记住它代表十进制的 10。
- 分组方向:当二进制转十六进制时,分组必须从右向左开始。如果总位数不是4的倍数,要在最左边补0。例如,二进制 10110,应分组为 0001 0110,而不是 1011 0...。所以它是 16(十六进制),而不是 B...。
本节引入了十六进制,解释了它使用 0-9 和 A-F 共16个数码。其存在的根本原因在于 $16=2^4$ 的关系,使得一个十六进制位可以简洁、完美地代表四个二进制位。这让它成为程序员读写长串二进制数据(如内存地址、机器码)的理想速记工具。
这部分的存在是为了“提供一种人类友好的二进制表示法”。直接读写一长串 0 和 1 对人类来说既困难又容易出错。十六进制作为一种紧凑的“二进制速记”,极大地提高了程序员的工作效率和代码的可读性,是连接人类思维和机器底层表示的重要桥梁。
[直觉心- 10
📜 [原文13]
1410. 带负数表示的模运算
- 对于 $\mathrm{X} \bmod \mathrm{Y}$,我们通常将余数定义为 0 到 $\mathrm{Y}-1$ 之间的值
- 有用的替代方法:将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 例如,$\bmod 8$ 将使用 -4 到 3 的余数值:
- 注意:
- 7 变为 -1(它们在 $\bmod 8$ 下是相同的)
- 6 变为 -2(在 $\bmod 8$ 下也相同)
- 一直到 4 变为 -4(在 $\bmod 8$ 下相同)
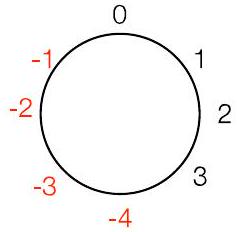
“风车”表示法:对正数顺时针移动,
对负数逆时针移动
- 有用的替代方法:将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 在此替代表示法中, $10 \bmod 8$ 是多少?
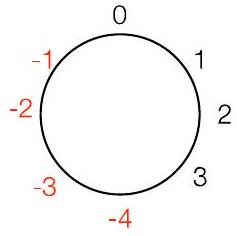
“风车”表示法:对正数顺时针移动,对负数逆时针移动
这个风车是用于 $\bmod 8$ (范围 $\mathbf{- 4}$ 到 $\mathbf{3}$ )
对 2 的补码很重要(稍后讨论)
这一节引入了一种处理模运算的另类但非常重要的方法,它直接关系到计算机中最常用的负数表示法——2的补码。
- 标准余数定义:首先回顾了标准的模运算定义,即 $X \bmod Y$ 的结果(余数)总是在 $[0, Y-1]$ 这个区间内。这是一个非负整数。例如 $10 \bmod 8 = 2$,$-1 \bmod 8 = 7$。
- 有用的替代方法:这里提出了一个新的规则:将余数的范围定义在 $[-\frac{Y}{2}, \frac{Y}{2}-1]$ 这个对称的区间内。这个区间的中心是0,包含了负数。
- 这个定义要求 $Y$ 是偶数,这在计算机中总是成立的,因为 $Y$ 通常是 $2^k$。
- $\bmod 8$ 的例子:
- $Y=8$。
- 标准范围是 $[0, 7]$。
- 替代范围是 $[-\frac{8}{2}, \frac{8}{2}-1] = [-4, 3]$。
- 值的映射关系:
- 在新的表示法下,一些原本是大的正数,现在被映射为小的负数。
- 7 变为 -1:因为 $7 = 1 \times 8 + (-1)$。在模8的意义下,7和-1是等价的(它们在风车上同一个位置)。从0顺时针走7步,和逆时针走1步,终点相同。
- 6 变为 -2:因为 $6 = 1 \times 8 + (-2)$。
- 5 变为 -3:因为 $5 = 1 \times 8 + (-3)$。
- 4 变为 -4:因为 $4 = 1 \times 8 + (-4)$。
- 而 0, 1, 2, 3 保持不变。
- 图片分析:...-09.jpg 和 ...-10.jpg 的风车图直观地展示了这个新的范围。风车的上半部分是 0, 1, 2, 3,下半部分不再是 4, 5, 6, 7,而是 -4, -3, -2, -1。这就像把钟表的 7, 8, 9, 10, 11 点重新标记为 -5, -4, -3, -2, -1 点。
- $10 \bmod 8$ 在新方法下是多少?
- $10 = 1 \times 8 + 2$。余数是 2。
- 2 落在 $[-4, 3]$ 的范围内,所以结果仍然是 2。
- 在风车上,从0开始顺时针走10步,最终停在 2 的位置。
- 对2的补码很重要(稍后讨论):这是本节的点睛之笔。教授明确指出,引入这种奇怪的负数余数范围,不是为了数学游戏,而是因为它完美地描述了2的补码系统的行为。
- 在一个k位的2的补码系统中,所有计算都是在 $\bmod 2^k$ 下进行的。
- 其表示的数值范围恰好是 $[ -2^{k-1}, 2^{k-1}-1 ]$。
- 例如,对于3位系统 ($k=3$),$\bmod 8$,表示范围是 $[-4, 3]$,这与我们刚刚讨论的 $\bmod 8$ 的替代余数范围完全一致!
- 100 表示-4, 101 表示-3, 110 表示-2, 111 表示-1。
- 000 表示0, 001 表示1, 010 表示2, 011 表示3。
- 示例1:计算 $15 \bmod 8$ 在两种表示法下的值。
- 标准表示法:$15 = 1 \times 8 + 7$。结果是 7。
- 替代表示法:我们希望余数在 $[-4, 3]$。$15 = 2 \times 8 - 1$。所以结果是 -1。在风车上,从0顺时针走15步,停在 7 的位置,也就是 -1 的位置。
- 示例2:计算 $-5 \bmod 8$ 在两种表示法下的值。
- 标准表示法:$-5 = -1 \times 8 + 3$。结果是 3。
- 替代表示法:结果 3 已经落在 $[-4, 3]$ 区间内。所以结果也是 3。
- 示例3:计算 $4 \bmod 8$ 在两种表示法下的值。
- 标准表示法:$4 = 0 \times 8 + 4$。结果是 4。
- 替代表示法:我们希望余数在 $[-4, 3]$。4 不在这个区间。但我们知道 $4 = 1 \times 8 - 4$。所以结果是 -4。
- 边界值 Y/2 的归属:在区间 $[-\frac{Y}{2}, \frac{Y}{2}-1]$ 中,正边界 $\frac{Y}{2}-1$ 不包含 $\frac{Y}{2}$,而负边界包含 $-\frac{Y}{2}$。例如,在 $\bmod 8$ 中,范围是 $[-4, 3]$,可以表示 -4,但不能表示 +4。这导致了不对称性,负数比正数多一个。这正是2的补码的特性。
- 何时使用何种表示法:必须清楚,这只是对模运算结果的一种“解读”方式。标准的非负余数定义在纯数学中更常用。而这种包含负数的对称范围定义,则是理解计算机有符号数运算的“专用镜头”。
本节介绍了模运算的一种替代余数表示法,即将余数范围从标准的 $[0, Y-1]$ 调整为对称的 $[-\frac{Y}{2}, \frac{Y}{2}-1]$。通过 $\bmod 8$ 的例子,展示了如何将大的正余数映射为小的负余数。最关键的是,这种表示法与2的补码的数值范围和运算行为天然吻合,为后续理解计算机如何处理负数运算提供了重要的数学模型。
这部分的存在是为了“建立2的补码的数学心智模型”。与其直接抛出2的补码的位操作规则(取反加一),不如先从更抽象的模运算角度,让学生理解“在有限的、循环的数字空间里,正数和负数是如何等价和转换的”。这为2的补码提供了一个坚实的“为什么”,而不仅仅是“是什么”和“怎么做”。
想象一个钟表,但我们重新标记它。正常的钟表是 0 到 11 点。
- 标准模12:就是这个 0-11 的范围。
- 替代模12:范围是 $[-6, 5]$。我们可以把 11 点看作 -1 点(差1分钟到整点),10 点看作 -2 点... 7 点看作 -5 点,而 6 点必须看作 -6 点。这样,从 1 点到 5 点是“顺时针走的短路”,从 7 点到 11 点是“逆时针走的短路”。
想象一条首尾相连的跑道,总长800米,每隔100米有一个标记点(0, 100, 200, ..., 700)。
- 标准模800:你跑了1000米,你的位置在 200 米处 ($1000 \bmod 800 = 200$)。
- 替代模800:范围是 [-400, 300]。现在,我们把 700 米标记点重新命名为 -100 米(离终点/起点差100米),600 米点命名为 -200 米... 400 米点命名为 -400 米。
- 你跑了 700 米,你的位置是 700,但也可以说是 -100。对裁判来说,喊 -100 更容易,因为他知道你离终点很近了。
- 你跑了 1000 米,位置在 200 米处。这个值在 [-400, 300] 范围内,所以你的位置就是 200。
- 你跑了 -100 米(后退100米),你的位置是 700 米。在替代表示法下,它也可以被看作 -100 米。
15行间公式索引
- 十进制数4537.8的按权展开求和表示:
- 第二次出现的十进制数4537.8按权展开求和表示:
- 二进制数1011.1转换为十进制的按权展开表示:
- 第二次出现的二进制数1011.1转换为十进制的按权展开表示:
- 十六进制数26BA转换为十进制的按权展开表示(格式1):
- 十六进制数26BA转换为十进制的按权展开表示(格式2):
- 二进制分组与十六进制位权的数学关系示例:
- 无符号二进制加法示例(30+21):
- 溢出的二进制加法结果(30+21=19):
- 二进制加法在有符号幅度和1的补码下的问题示例:
- 二进制加法在有符号幅度下的计算过程(5+(-5) != 2):
- 二进制加法在有符号幅度下的错误结果展示(5+(-5)=2):
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。