117. 数字编码
| 无符号 | 符号 & 幅度 | 1 的补码 | 2 的补码 | |
|---|---|---|---|---|
| 000 | 0 | +0 | +0 | +0 |
| 001 | 1 | +1 | +1 | +1 |
| 010 | 2 | +2 | +2 | +2 |
| 011 | 3 | +3 | +3 | +3 |
| 100 | 4 | 0 | -3 | -4 |
| 101 | 5 | -1 | -2 | -3 |
| 110 | 6 | -2 | -1 | -2 |
| 111 | 7 | -3 | 0 | -1 |
| 8个值 | 7个值,2 个零 | 7个值,2 个零 | 8个值,1 个零 |
有符号幅度和 1 的补码浪费了一个位模式:2 个表示 0
| 无符号 | 符号 & 幅度 | 1 的补码 | 2 的补码 | |
|---|---|---|---|---|
| 000 | 0 | +0 | +0 | +0 |
| 001 | 1 | +1 | +1 | +1 |
| 010 | 2 | +2 | +2 | +2 |
| 011 | 3 | +3 | +3 | +3 |
| 100 | 4 | -0 | -3 | -4 |
| 101 | 5 | -1 | -2 | -3 |
| 110 | 6 | -2 | -1 | -2 |
| 111 | 7 | -3 | -0 | -1 |
| 8个值 | 7个值,2 个零 | 7个值,2 个零 | 8个值,1 个零 |
117.1 数字编码
| 2 的补码:最小的负数在表示中没有正数对应 翻转位并加 1 的过程不能成功地取反该数字 | ||||
|---|---|---|---|---|
| 无符号 | 符号 & 幅度 | 1 的补码 | 2 的补码 | |
| 000 | 0 | +0 | +0 | +0 |
| 001 | 1 | +1 | +1 | +1 |
| 010 | 2 | +2 | +2 | +2 |
| 011 | 3 | +3 | +3 | +3 |
| 100 | 4 | 0 | -3 | -4 |
| 101 | 5 | -1 | -2 | -3 |
| 110 | 6 | -2 | -1 | -2 |
| 111 | 7 | -3 | 0 | -1 |
| 8个值 | 7个值,2 个零 | 7个值,2 个零 | 8个值,1 个零 |
在 2 的补码中,二进制加法算法总是有效的(除非发生溢出)!
217.2 使用二进制加法算法
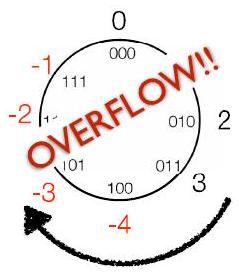
当发生溢出时,结果将差 $2^{\text{字长}}$
218. 2 的补码的特殊之处
- 与无符号数类似,当使用 BAA 进行加法时,结果在 $\bmod 2^{\mathrm{k}}$ 下是正确的( $k$ 是字长)
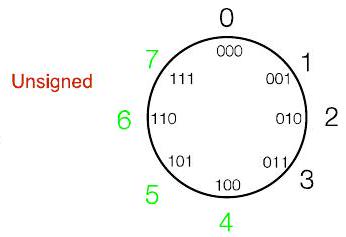
- 无论是无符号还是 2 的 补码形式,都将落在模 $2^{k}$ 正确的值上,但如果不在风车上则实际值不正确
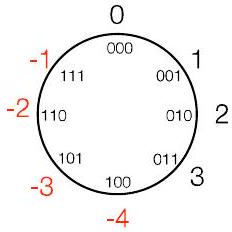
- 思考模运算(例如,$\bmod 8$)
- 如果我们选择“无符号” $\bmod 8 = (0,1,2,3,4,5,6,7)$
- $3+6 \bmod 8=1$(即 $\text{余数}(9/8)$)
- $3-6 \bmod 8=5$
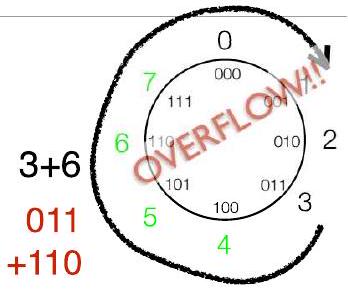
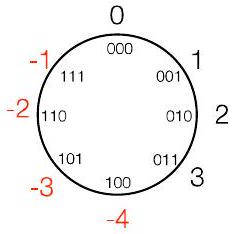
118.1 模运算与溢出的关联
- 思考模运算(例如,$\bmod 8$)
- 如果我们选择“无符号” $\bmod 8 = (0,1,2,3,4,5,6,7)$
- $3+6 \bmod 8=1$(即 $\text{余数}(9/8)$)
- $3-6 \bmod 8=5$(也溢出)
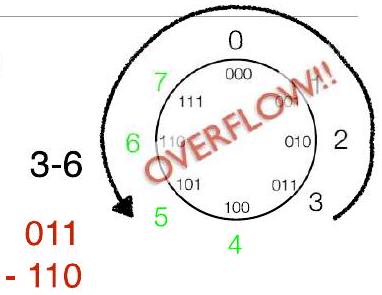
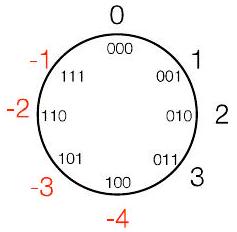
218.2 补码环形表示(风车)
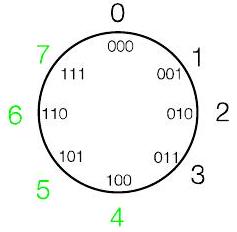
- 但也可以选择“2 的 补码” $\bmod 8 = (-4,-3,-2,-1,0,1,2,3)$
- 6(即 110)将变为 -2
- $3+(-2) \bmod 8 = 3-2 \bmod 8 = 1$
- $3-(-2) \bmod 8 = 3+2 \bmod 8 = -3$
011
+110
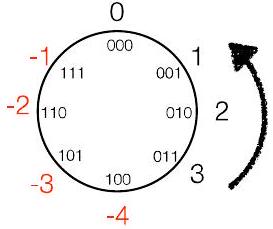
318.3 C语言中的补码示例
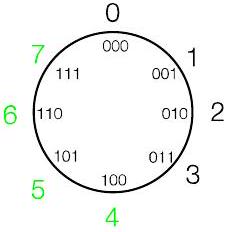
- 但也可以选择“2 的 补码” $\bmod 8 = (-4,-3,-2,-1,0,1,2,3)$
011
- 6(即 110)将变为 -2
- $3+(-2) \bmod 8 = 3-2 \bmod 8 = 1$
- $3-(-2) \bmod 8 = 3+2 \bmod 8 = -3$
```
int main() {
int x = 47;
int y=-50;
unsigned int z = 50;
printf("%d %d %uln", x, y, z);
}
```
你(无意中)在哪里使用过 2 的补码?
```
int main() {
int x = 47;
int y=-50;
unsigned int z = 50;
printf("%d %d %uln", x, y, z);
}
- The computer represents
- x and y as signed 2 's complement
- $z$ as an unsigned
- C Demo: https://onlinegdb.com/49zlpDA9P8
- Note:
- $0 \times F$ (in Hex) is $15=1111$ in (unsigned) binary
- $0 \times 8$ (in Hex) is $8=1000$ in (unsigned) binary
- $2^{32}=4,294,967,296$ and $2^{31}=2,147,483,648$
```
418.4 “翻转位+1”的直观解释
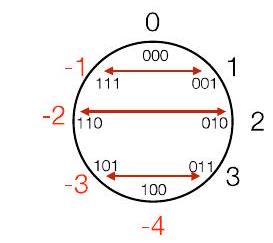
负值正好在对面
2 的补码

所有位翻转的值比正好在对面的值顺时针少 1 刻度
518.5 “翻转位+1”的正式证明
- 从任何 $k$-位字 $X$(除了 $100 \ldots 000$)开始,并以 2 的补码表示它
- 设 $Y = X$ 并翻转所有位
- $X+Y=11 \ldots 1111$(使用二进制加法算法)
- 因此,$X+Y=-1$ 在 2 的补码表示中(在“风车”上从 $00 \ldots 0000$ 逆时针旋转 1 位)
- 然后 $X+Y+1=00 \ldots 0000$(使用二进制加法算法)
- 所以 $Y+1=-X$(并且回想 $Y$ 是 $X$ 翻转所有位)
319. 表示 vs. 操作
119.1 k-位字 & 各种表示的范围
- 给定一个 $k$-位字,可以表示的数字范围是:
- 无符号:0 到 $2^{k}-1$(例如,$k=8$,0 到 255)
- 有符号幅度:$-2^{k-1}+1$ 到 $2^{k-1}-1$(例如,$k=8$,-127 到 127 [2 种表示 0 的方式])
- 1 的补码:与有符号幅度相同(但负数表示方式不同)
- 2 的补码:$-2^{k-1}$ 到 $2^{k-1}-1$(例如,$k=8$,-128 到 127 [1 种表示 0 的方式])
420. 获取表示
- 问:给定 8-位字长,10001011 的值是多少?
120.1 获取表示
- 问:给定 8-位字长,10001011 的值是多少?
- 答:它是以无符号、有符号幅度、1 的补码还是 2 的补码表示?
- 无符号:$128+8+2+1=139$
- 有符号幅度:$-1 * (8+2+1)=-11$
- 1 的补码:01110100 的取反 $=-116$
- 2 的补码:01110101 的取反 $=-117$
- 注意:对于给定的一组位,当 \# 为负数时,2 的补码比 1 的补码小 1
521. 表示 vs. 操作 (总结)
- 我们已经讨论了表示整数的各种方法
- 无符号、有符号幅度、1 的补码、2 的补码
- 还有以位为单位的操作,名称相同
- 1 的补码操作:翻转所有位
- 2 的补码操作:翻转所有位并(BAA)加 1
- 操作可以在数字上执行,无论表示形式如何
- 例如,设 10111 是一个有符号幅度形式的数字(值为 -7)
- 在 10111 上执行 2 的补码(操作) $=01001$(在有符号幅度形式中值为 9)
- 观察:
- 当数字使用 2 的补码表示时,2 的补码操作会取反该数字
- 当数字使用 1 的补码表示时,1 的补码操作会取反该数字
622. 自动化减法
- 问:为什么我们对 2 的补码感兴趣,尽管它看起来如此不直观?
- 答:自动化减法(即加符号相反的 \#)要容易得多
- 例如,字长 6,使用有符号幅度表示执行 14-21
122.1 自动化减法示例
- 问:为什么我们对 2 的补码感兴趣,尽管它看起来如此不直观?
- 答:自动化减法(即加符号相反的 \#)要容易得多
- 例如,字长 6,使用有符号幅度表示执行 14-21
- 有符号幅度有很多潜在的“繁重工作”
- 例如,翻转顶部 & 底部,“从较高位借位”等。
723. 2 的补码减法:利用 BAA
- 只需取反减数(减法中的底数)并加
- 例如,字长 6,使用 2 的补码表示执行 14-21
123.1 补码减法示例
- 只需取反减数(减法中的底数)并加
- 例如,字长 6,使用 2 的补码表示执行 14-21
2 的补码减法:利用 BAA
- 只需取反减数(减法中的底数)并加
- 例如,字长 6,使用 2 的补码表示执行 14-21

$X=111001, -X=000111=7, X=-7$
824. 检测溢出
- 问:如何判断计算结果是否溢出(即结果无法在字长约束内表示)
- 例如,4-位字,无符号:1110 + $1010 (14 + 10)$
- 结果是 24,无法在 4-位无符号中表示(只有 0-15 的值)
- 因此,溢出
- 无符号检测容易:
- 加法溢出
对于无符号 | 111 |
| :--- |
|---|
| $\underline{1010}$ |
| 1000 |
- 减法:减数大于 \#(结果为负),则溢出
925. 2 的补码中的溢出检测很简单
| -如果最终两个进位匹配,则没有溢出 - 如果不同,则溢出 - 例如,字长 $=4$ |
|||
|---|---|---|---|
| $5+1=6$ | $-5+-3=-8$ | $-2+7=5$ | $-2+-7=-9$ |
| 00 | 11 | 11 | 10 |
| + | + | + | + |
| $\underline{0001}$ | $\underline{1101}$ | 0111 | $\underline{1001}$ |
| 0110 | 1000 | 0101 | 0111 |
- 需要考虑 3 种情况:
- 两个 \# 都是正数(即最高位都是 0)
- 两个 \# 都是负数(即最高位都是 1)
- 一个是正数(最高位 0),另一个是负数(最高位 1)
1026. 为什么 2 的补码溢出检测有效的证明
- 情况 1:两者皆正:
- 写下两个最高位进位为 A 和 B
- 写下两个最高位进位为 $A$ 和 $B \quad A B$
- $A=$ 进位 B $+0+0 O X_{k-2} X_{k-3} \ldots X_{0}$
$O Y_{k-2} Y_{k-3} \ldots Y_{0}$
- A 始终为 0!
- 最高位 $= B+0+0$
- $B=1$:将结果解释为负数?
错误
- $B=0$:正常(刚刚执行了无符号 $K-1$ 位
加法)
126.1 情况2:两者皆负
- 情况 2:两者皆负:
- 写下两个最高位进位为 A 和 B
- $A=$ 进位 B $+1+1$
- A 始终为 1!
- 最高位 = B + 1 + 1
- $B=0$:最高位 = 0:正数 \#?错误
- $B=1$:负数:正常(并且 $\bmod 2^{\mathrm{k}}$ 正确)
226.2 情况3:一正一负
- 情况 3:一个正数,另一个负数:
- 写下两个最高位进位为 $A$ 和 $B+X_{k-2} X_{k-3} \ldots X_{0}$
- $A=$ 进位 $(B+1): B=0 \rightarrow A=0, B=1 \rightarrow A=1 \quad 1 Y_{k-2} Y_{k-3} \ldots Y_{0}$
- 所以永远不会溢出?
- 没错!
- 注意 $X+(-Y)$ 将小于 $X$ 且大于 $-Y$
- 如果 $X$ 可以用 2 的补码表示,并且 $-Y$ 可以用 2 的补码表示,那么任何 $Z$ 在 $-Y \leq Z \leq X$ 之间也都可以表示。
- 不能过分强调溢出意味着结果无法在字长内表示(不一定是结果太大)!
- 示例:假设我选择一个(奇怪的)方式将 2-位字映射到值,如下所示:
| 两位字 word |
关联值 Value |
|---|---|
| 00 | 1 |
| 01 | 3 |
| 10 | 6 |
| 11 | 2 |
1127. 关于溢出的最后思考
- 不能过分强调溢出意味着结果无法在字长内表示(不一定是结果太大)!
- 示例:假设我选择一个(奇怪的)方式将 2-位字映射到值,如下所示:
| 两位字 word |
关联值 Value |
|---|---|
| 00 | 1 |
| 01 | 3 |
| 10 | 6 |
| 11 | 2 |
127.1 溢出示例分析
- 不能过分强调溢出意味着结果无法在字长内表示(不一定是结果太大)!
- 示例:假设我选择一个(奇怪的)方式将 2-位字映射到值,如下所示:
| 两位字 word |
关联值 Value |
|---|---|
| 00 | 1 |
| 01 | 3 |
| 10 | 6 |
| 11 | 2 |
$1+3$ 应该等于 4,但没有 2-位组合表示 4
因此,对于此表示,00+01 导致溢出
1228. 浮点
1329. 需要更大的范围?浮点表示
- 改变编码。
- 浮点(用于以紧凑方式表示非常大的数字)
- 很像科学记数法:
尾数
注意:尾数总是采用 X.XX... 形式
(又名小数部分)
(小数点前一位)
129.1 浮点表示示例
- 改变编码。
- 浮点(用于以紧凑方式表示非常大的数字)
- 很像科学记数法:
尾数
注意:尾数总是采用 X.XX... 形式
(又名小数部分)
(小数点前一位)
- 但对于本课程,请考虑二进制:
注意:在正确形式中,对于二进制,尾数总是 1.XX... (小数点前一位,且该位总是 1)
唯一例外:$0=0.0 \times 2^{0}$
1430. 浮点数的标准形式
- 如何在 32-位字的限制内表示浮点数
- 字的位分成不同的字段
3130292827262524232221201918171615141312111009080706050403020100
符号 小数部分 (尾数)
- IEEE 754 标准规定
- 哪些位表示哪些字段(位 31 是符号位,位 30-23 是 8-位指数,位 22-00 是 23-位小数部分)
- 如何解释每个字段
1531. IEEE 754 浮点描述
3130292827262524232221201918171615141312111009080706050403020100
| $\frac{5}{5}$ | 指数 | 小数部分 (尾数) |
|---|
- 符号:0 = 正数 \#,1 = 负数 \#(像有符号幅度)
- 指数:无符号,偏移量为 127
- 指数值 = 8 位无符号二进制表示 -127
- 小数部分:回想小数部分总是 1.XXXXXX 形式
- 省略‘1’,只表示“XXXXXXX”部分
3130292827262524232221201918171615141312111009080706050403020100
1000011011010000000000000000000
- $=(-1) \times 1.101_{(2)} \times 2^{13-127}=-1.625_{(10)} \times 2^{-114}=-7.82409 \times 10^{-35}$
- 因为表示总是 $\pm 1.\mathrm{XXXX} \times 2^{\text{yyy}}$ 形式,不能表示真正的 0
- 注意:所有位都设为 0 等于 $1.0 \times 2^{-127}$,一个非常非常小的数字,实际上是 0
1632. 偏移量和浮点数比较
- 偏移量允许指数在 -127(非常小)和 128(非常大)之间
- 问:为什么使用偏移量而不是 2 的补码或无符号幅度?
- 答:比较两个浮点数 A & B 哪个更大很容易
- 步骤 1:检查符号。A 为正,B 为负,返回 A > B。A 为负,B 为正,返回 A < B
132.1 步骤2:检查指数
- 偏移量允许指数在 -127(非常小)和 128(非常大)之间
- 问:为什么使用偏移量而不是 2 的补码或无符号幅度?
- 答:比较两个浮点数 A & B 哪个更大很容易
- 步骤 1:检查符号。A 为正,B 为负,返回 A > B。A 为负,B 为正,返回 A < B
- 步骤 2 (A 和 B 符号相同): 检查指数
- (A 为正且 A.指数 > B.指数) 或 (A 为负且 A.指数 < B.指数),返回 A > B
- (A 为负且 A.指数 > B.指数) 或 (A 为正且 A.指数 < B.指数),返回 A < B
232.2 步骤3:检查小数部分
- 偏移量允许指数在 -127(非常小)和 128(非常大)之间
- 问:为什么使用偏移量而不是 2 的补码或无符号幅度?
- 答:比较两个浮点数 A & B 哪个更大很容易
- 步骤 1:检查符号。A 为正,B 为负,返回 A > B。A 为负,B 为正,返回 A < B
- 步骤 2 (A 和 B 符号相同): 检查指数
- (A 为正且 A.指数 > B.指数) 或 (A 为负且 A.指数 < B.指数),返回 A > B
- (A 为负且 A.指数 > B.指数) 或 (A 为正且 A.指数 < B.指数),返回 A < B
- 步骤 3 (A 和 B 符号相同,指数相同): 检查小数部分
- (A 为正且 A.小数部分 > B.小数部分) 或 (A 为负且 A.小数部分 < B.小数部分),返回 A > B
- (A 为负且 A.小数部分 > B.小数部分) 或 (A 为正且 A.小数部分 < B.小数部分),返回 A < B
332.3 步骤4:完全相等与有符号比较的相似性
- 偏移量允许指数在 -127(非常小)和 128(非常大)之间
- 问:为什么使用偏移量而不是 2 的补码或无符号幅度?
- 答:比较两个浮点数 A & B 哪个更大很容易
- 步骤 1:检查符号。A 为正,B 为负,返回 A > B。A 为负,B 为正,返回 A < B
- 步骤 2 (A 和 B 符号相同): 检查指数
- (A 为正且 A.指数 > B.指数) 或 (A 为负且 A.指数 < B.指数),返回 A > B
- (A 为负且 A.指数 > B.指数) 或 (A 为正且 A.指数 < B.指数),返回 A < B
- 步骤 3 (A 和 B 符号相同,指数相同): 检查小数部分
- (A 为正且 A.小数部分 > B.小数部分) 或 (A 为负且 A.小数部分 < B.小数部分),返回 A > B
- (A 为负且 A.小数部分 > B.小数部分) 或 (A 为正且 A.小数部分 < B.小数部分),返回 A < B
- 步骤 4 (A 和 B 符号相同,指数相同,小数部分相同): 返回 A = B
- 观察:当位按照符号、指数、幅度排序时,过程与比较 2 个有符号幅度数相同
哪个 IEEE 754 FP \# 最大?

- 所有 + \#s,$B > A$(指数更大),$B > C$(指数相同,小数部分更大)
- 如果 \#s 简单地视为有符号幅度,会怎样?
- 结果相同:$B > C > A$
1733. IEEE 754 64-位 (双精度)
- 在 32-位架构中描述为两个 32-位字
| 字 1 | 31/30292827262524232221201918171615141312111009080706050403020100 | |
|---|---|---|
| 指数 | 小数部分 (高位) |
3130292827262524232221201918171615141312111009080706050403020100
字 2 小数部分 (低位)
- 11-位指数,偏移量为 1023
- 小数部分长 52 位(字 1 中 20 个高位,字 2 中剩余 32 个低位)
1834. 下溢
- 当值的幅度太小而无法用表示形式描述时
- 例如,在 IEEE 754 浮点中:
- $X = 1 \times 2^{-100}$ 可以通过标准表示(指数字段中的位集是什么?)
- 但是,$X^2$ 等于 $2^{-200}$ 太小,无法表示
- 最小可能指数是 -127
- 因此,尝试计算 $X*X$ 会导致下溢
1935. 讲座结束
- 课程其余部分的重要要点:
- 计算机的高层视角(数字化视角):字长这一概念
- 二进制数:负数表示法(二进制补码)
- 加法、减法、溢出、溢出检测