11. 数字编码
📜 [原文1]
| 无符号 | 符号 & 幅度 | 1 的补码 | 2 的补码 | |
|---|---|---|---|---|
| 000 | 0 | +0 | +0 | +0 |
| 001 | 1 | +1 | +1 | +1 |
| 010 | 2 | +2 | +2 | +2 |
| 011 | 3 | +3 | +3 | +3 |
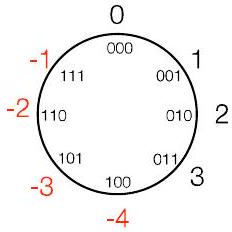
| 100 | 4 | 0 | -3 | -4 |
| 101 | 5 | -1 | -2 | -3 |
| 110 | 6 | -2 | -1 | -2 |
| 111 | 7 | -3 | 0 | -1 |
| 8个值 | 7个值,2 个零 | 7个值,2 个零 | 8个值,1 个零 |
这段内容通过一个表格,对比了四种不同的方法来用3个二进制位(bit)表示数字。这四种方法分别是无符号(Unsigned)、符号与幅度(Sign & Magnitude)、1的补码(1's Complement)和2的补码(2's Complement)。理解这些表示法是理解计算机内部如何处理和存储数字的基础。
- 二进制位(Binary Digits, bits):计算机的基本存储单位,每个位只能是0或1。用3个位,我们可以组合出 $2^3 = 8$ 种不同的模式,从 000 到 111。
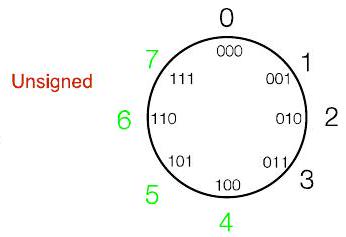
- 无符号 (Unsigned) 表示法:这是最直接的表示法。它将每个二进制模式直接映射到一个非负整数。转换规则是标准的二进制转十进制。例如,110 被解释为 $1 \cdot 2^2 + 1 \cdot 2^1 + 0 \cdot 2^0 = 4 + 2 + 0 = 6$。使用3个位,它可以表示从0 (000) 到7 (111) 的8个不同的非负整数。
- 符号与幅度 (Sign & Magnitude) 表示法:为了表示负数,这种方法将最高位(最左边的位)用作符号位。0 代表正数(+),1 代表负数(-)。剩下的位则表示幅度(绝对值),其转换规则与无符号数相同。例如,011 中,最高位是 0(正),剩下的 11 表示3,所以整个数是 +3。对于 101,最高位是 1(负),剩下的 01 表示1,所以整个数是 -1。
- 一个显著的缺点是存在两个零的表示:000 (+0) 和 100 (-0)。这不仅浪费了一个位模式,还给算术运算带来了复杂性。
- 1的补码 (1's Complement) 表示法:这种方法对正数的表示与符号与幅度法相同。对于负数,它的表示是通过将对应正数的所有位进行按位取反(0变1,1变0)得到的。例如,+3 是 011。要得到 -3,我们将 011 的每一位取反,得到 100。
- 和符号与幅度法一样,1的补码也存在两个零:000 (+0) 和 111 (-0),因为 111 是 000 按位取反的结果。
- 2的补码 (2's Complement) 表示法:这是现代计算机中最普遍使用的有符号整数表示法。正数的表示与前两种有符号表示法相同。负数的表示规则是“按位取反,再加1”。例如,要得到 -3,我们先取 +3 的二进制 011,按位取反得到 100,然后再加1,得到 101。
- 2的补码的最大优点是它只有一个零的表示(000)。这使得它可以比前两种方法多表示一个负数(在这个3位的例子中是-4)。同时,它的加减法运算可以统一处理,无需关心操作数的符号,大大简化了硬件设计。
表格最后一行总结了每种表示法的效率:
- 无符号、2的补码:能够表示8个不同的值。
- 符号与幅度、1的补码:由于存在两个零的表示,它们只能表示7个不同的值。
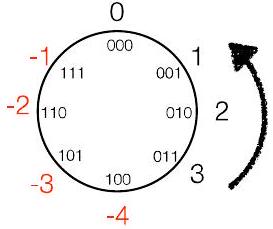
- 示例1:解释二进制模式 110
- 在无符号表示法中:$1 \cdot 2^2 + 1 \cdot 2^1 + 0 \cdot 2^0 = 4 + 2 + 0 = 6$。
- 在符号与幅度表示法中:最高位是 1,表示负号。剩下的 10 表示 $1 \cdot 2^1 + 0 \cdot 2^0 = 2$。所以,110 代表 -2。
- 在1的补码表示法中:由于最高位是 1,它是一个负数。为了找出它的值,我们先将其按位取反得到 001,这个值是 +1。所以,110 是 -1。
- 在2的补码表示法中:由于最高位是 1,它是一个负数。为了找出它的值,我们先减1得到 101,再按位取反得到 010,这个值是 +2。所以,110 是 -2。另一种更快的计算负数的方法是:最高位 1 代表 $-2^{3-1} = -4$,所以 110 的值是 $-4 + (1 \cdot 2^1 + 0 \cdot 2^0) = -4 + 2 = -2$。
- 示例2:表示数字 -1
- 在符号与幅度表示法中:符号为负,所以最高位是 1。幅度是 1,用剩下的2位表示为 01。所以,-1 是 101。
- 在1的补码表示法中:我们先找到 +1 的表示,即 001。然后按位取反,得到 110。
- 在2的补码表示法中:我们先找到 +1 的表示,即 001。按位取反得到 110,然后加1,得到 111。
- 零的表示:最大的易错点在于符号与幅度和1的补码中对零的两种表示(+0 和 -0)。这常常导致混淆,并且是这两种表示法在实际中较少使用的原因之一。
- 范围不对称:在2的补码中,负数的范围比正数多一个。例如,在3位系统中,可以表示-4 (100),但不能表示+4。这个最负的数(-4)没有对应的正数。
- 负数转换:计算2的补码负值时,初学者常常忘记“取反后还要加1”这一步。或者在从负的2的补码转换回十进制时,使用错误的逆向操作。正确的逆向操作是“先减1,再取反”或使用权重法。
- 最高位:在有符号表示中,最高位(MSB)是符号位,不能像无符号数那样简单地计入数值。例如 100 在无符号下是4,但在2的补码下是-4。
该表格核心展示了使用有限二进制位表示数字的四种基本编码方案。它清晰地揭示了无符号数、符号与幅度、1的补码和2的补码之间的区别,特别是它们在表示范围和零的表示上的差异。2的补码因其唯一的零表示和简化的算术逻辑,成为现代计算机系统的事实标准。
本节的目的是介绍数字在计算机内的底层表示方法。计算机硬件只能处理0和1,因此必须有一套规则来解释这些二进制序列代表的数值。理解这些不同的表示法,尤其是2的补码,对于理解算术运算、数据类型范围、溢出等计算机系统核心概念至关重要。
- 无符号:想象一把只有正数刻度的尺子,从0开始。
- 符号与幅度:想象一把中间是0点,向两边对称延伸的尺子。但是这把尺子很奇怪,0点有两个标签,一个叫"+0",一个叫"-0"。
- 1的补码:也像一把对称的尺子,同样有两个0点。可以想象成一个钟表,但0点和对面的点(比如6点)都被特殊标记了。
- 2的补码:想象一个环形的里程表或一个钟表。从0开始顺时针走是正数(1, 2, 3...)。当走到一半(比如12点走到6点的位置)后,继续走就进入了负数区域。比如,从0逆时针走1步是-1,这个位置恰好是顺时针走到底的位置。这个环是连续的,没有重复的刻度。
想象你有一个只能显示3个灯泡(亮/灭)的装置。
- 无符号:你用它来数数,从0(全灭)到7(全亮)。
- 符号与幅度:你规定第一个灯泡是“颜色灯”,绿色代表加号,红色代表减号。剩下两个灯泡表示数量。但你发现“绿灯+两个灭灯”和“红灯+两个灭灯”都表示没有东西,有点浪费。
- 1的补码:你发明了一种“反色”规则来表示负数。正数是一种颜色组合,负数是完全相反的颜色组合。但你还是发现“全绿”和“全红”这两个状态都代表“无”,还是很别扭。
- 2的补码:你终于找到了一个聪明的办法。你把这些灯泡排列成一个圈,像钟表一样。从“全灭”开始,每亮一个灯泡,数字就加一。转了半圈后,你规定剩下的模式都代表负数,并且它们正好无缝地接回了起点。这样,8种模式,8个不同的数字,完美!
📜 [原文2]
有符号幅度和 1 的补码浪费了一个位模式:2 个表示 0
| 无符号 | 符号 & 幅度 | 1 的补码 | 2 的补码 | |
|---|---|---|---|---|
| 000 | 0 | +0 | +0 | +0 |
| 001 | 1 | +1 | +1 | +1 |
| 010 | 2 | +2 | +2 | +2 |
| 011 | 3 | +3 | +3 | +3 |
| 100 | 4 | -0 | -3 | -4 |
| 101 | 5 | -1 | -2 | -3 |
| 110 | 6 | -2 | -1 | -2 |
| 111 | 7 | -3 | -0 | -1 |
| 8个值 | 7个值,2 个零 | 7个值,2 个零 | 8个值,1 个零 |
这段内容是前一个表格的变体和重申,旨在强调一个核心问题:符号与幅度(Sign & Magnitude)和1的补码(1's Complement)这两种有符号数表示法的固有缺陷。
- 核心论点: “有符号幅度和 1 的补码浪费了一个位模式:2 个表示 0”。这句话是本段的中心思想。在计算机中,每一个二进制模式都是宝贵的资源。如果有两个不同的模式代表同一个数学值(这里是0),那就意味着我们本可以用来表示另一个不同数字的模式被浪费了。
- 表格分析:
- 符号与幅度列:注意 000 被解释为 +0,而 100 被解释为 -0。这是因为在符号与幅度法中,最高位是符号位(0为正,1为负),其余位是幅度。当幅度为 00 时,无论符号位是 0 还是 1,数学上的值都是零。
- 1的补码列:注意 000 被解释为 +0,而 111 被解释为 -0。这是因为在1的补码中,负数是通过将对应正数的所有位取反得到的。+0 的表示是 000,将其所有位取反得到 111,这就成了 -0 的表示。
- 对比与结论:
- 2的补码列中,000 代表 +0,并且没有其他任何模式代表0。这使得它能够充分利用所有的位模式。
- 表格底部的总结再次强调了这一点:“7个值,2 个零” 对比 “8个值,1 个零”。对于一个3位的系统,符号与幅度和1的补码只能表示从-3到+3共7个不同的数值,而2的补码可以表示从-4到+3共8个不同的数值。
这个小小的差异在实际中会产生巨大的影响。拥有两个零的表示法会使算术逻辑单元(ALU)的设计变得复杂,因为在进行加减法后,需要额外检查结果是否为 +0 或 -0,并可能需要将它们统一为一种标准形式。而2的补码完全避免了这个问题,使得加法和减法可以用一套统一的、更简单的硬件逻辑来实现。
- 示例1: 4位系统中的零
- 在符号与幅度表示法中:
- +0 是 0000 (符号位0, 幅度0)
- -0 是 1000 (符号位1, 幅度0)
- 这里浪费了 1000 这个模式,它本可以用来表示其他数字。
- 在1的补码表示法中:
- +0 是 0000
- -0 是 1111 (对0000按位取反)
- 这里浪费了 1111 这个模式。
- 在2的补码表示法中:
- 0 就是 0000。没有 -0。模式 1000 在4位2的补码中代表-8,1111 代表-1。所有模式都得到了有效利用。
- 示例2: 值域范围比较 (8位系统,如 char 类型)
- 符号与幅度:
- 正数范围: 00000001 到 01111111,即 1 到 127。
- 负数范围: 10000001 到 11111111,即 -1 到 -127。
- 加上 +0 (00000000) 和 -0 (10000000),总共能表示 $127 + 127 + 1 = 255$ 个不同的值。等等,这里应该是能表示 $127 (正) + 127 (负) + 1 (零) = 255$ 个唯一值,但是用了 $256$ 个模式。问题就在于 0 有两个表示。所以实际唯一值的数量是 $2^8 - 1 = 255$ 个。
- 值的范围是 [-127, 127]。
- 2的补码:
- 正数范围: 00000001 到 01111111,即 1 到 127。
- 负数范围: 10000000 到 11111111,即 -128 到 -1。
- 加上 0 (00000000)。
- 总共能表示 $127 + 128 + 1 = 256$ 个不同的值。
- 值的范围是 [-128, 127]。
- 比较可见,2的补码利用了所有256个模式,并提供了一个不对称但更宽的表示范围。
- 误认为-0有特殊价值:学生可能会误以为 -0 在某些计算中有特殊用途。在绝大多数情况下,它只是一个冗余的表示,是表示法设计上的一个副作用。
- 混淆不同表示法的负数:在第二个表格中,100 在符号与幅度下是 -0,但在1的补码下是 -3。同一个二进制模式在不同表示法下含义完全不同,这是非常关键且容易出错的一点。
- 对“浪费”的理解:浪费的不仅仅是一个数字的表示,更是硬件资源的浪费和软件复杂度的增加。硬件需要额外的逻辑来处理这两种零,这会增加芯片面积、功耗和延迟。
本段通过一个 slightly modified 的表格,尖锐地指出了符号与幅度和1的补码表示法存在“双零”问题的缺陷。这个问题导致了位模式的浪费和算术实现的复杂化,从而反衬出2的补码表示法只有一个零、能表示更多数值的优越性。
这一部分的目的是在介绍了多种有符号数表示法之后,进行一次“优劣对比”,为后面只关注2的补码提供充分的理由。它回答了“为什么现代计算机几乎只用2的补码?”这个问题。通过强调其他方案的“浪费”,来凸显2的补码的“高效”。
想象你在分配房间号。你有8个房间,你想给8个不同的人住。
- 符号与幅度 / 1的补码的做法:你分配房间时,不小心把“0号”这个标签贴在了两个不同的房间门上(一个叫“正0号”,一个叫“负0号”)。结果,最后有个人没房间住,因为你浪费了一个房间。
- 2的补码的做法:你聪明地规划了房号,从-4到3,每个房间一个唯一的号码。8个房间,8个人,不多不少,完美入住。
想象一条数轴。
- 符号与幅度 / 1的补码的数轴:在0点的位置,有两个紧紧挨在一起的标记,一个“+0”,一个“-0”。这让数轴看起来有点“臃肿”和“不干净”。
- 2的补码的数轴:0点就是一个干干净净的点。但是数轴有点“不对称”,负半轴比正半轴长那么一点点。虽然不对称,但每个整数都有一个且仅有一个位置,非常清晰。
22. 数字编码
12.1. 2的补码的特殊负数
📜 [原文3]
| 2 的补码:最小的负数在表示中没有正数对应 翻转位并加 1 的过程不能成功地取反该数字 | ||||
|---|---|---|---|---|
| 无符号 | 符号 & 幅度 | 1 的补码 | 2 的补码 | |
| 000 | 0 | +0 | +0 | +0 |
| 001 | 1 | +1 | +1 | +1 |
| 010 | 2 | +2 | +2 | +2 |
| 011 | 3 | +3 | +3 | +3 |
| 100 | 4 | 0 | -3 | -4 |
| 101 | 5 | -1 | -2 | -3 |
| 110 | 6 | -2 | -1 | -2 |
| 111 | 7 | -3 | 0 | -1 |
| 8个值 | 7个值,2 个零 | 7个值,2 个零 | 8个值,1 个零 |
这段内容聚焦于2的补码表示法中的一个非常特殊的边界情况:最小的负数。
- 核心论点: “2 的补码:最小的负数在表示中没有正数对应”。在前面我们看到,3位2的补码的范围是-4到+3。其中,最小的负数是-4,它的二进制表示是 100。现在我们来看一下范围内的正数:1, 2, 3。显然,没有+4。这个范围是不对称的。
- 取反操作的失效: “翻转位并加 1 的过程不能成功地取反该数字”。我们知道,在2的补码中,对一个数取反(即正变负,负变正)的操作是“按位取反,再加1”。让我们对这个最小的负数 -4 (即 100) 尝试这个操作:
- 原始数: -4,二进制为 100。
- 第一步:按位取反: 100 按位取反得到 011。
- 第二步:加1: 011 加 1 得到 100。
- 结果: 我们惊讶地发现,对 -4 (100) 进行取反操作后,得到的结果仍然是 100 (-4)。也就是说,$-(-4)$ 应该等于 +4,但计算结果却是 -4。
- 原因: 这个现象的原因在于,+4 这个值超出了3位2的补码的表示范围。这个表示体系里根本就没有 +4 的位置。取反操作本身在模运算的意义下是正确的,但其结果 100 恰好就是我们对-4的定义,因此看起来就像“取反失败”了。这可以看作是一种特殊的溢出,即操作结果无法在当前的位数和表示法下正确表示。
- 表格佐证: 表格本身还是和之前一样,但这里的标题引导我们将注意力集中在2的补码列的 100 这个值上。它是 -4,是这个系统中绝对值最大的数。所有其他的非零数都有一个对应的相反数(例如 +1 (001) 和 -1 (111),+2 (010) 和 -2 (110),+3 (011) 和 -3 (101)),唯独 -4 (100) 是“孤独的”。
- 示例1: 4位2的补码系统
- 范围: $-2^{4-1}$ 到 $2^{4-1}-1$,即 -8 到 +7。
- 最小的负数是 -8,其二进制表示是 1000。
- 让我们对 -8 (1000) 取反:
- 按位取反: 1000 -> 0111。
- 加1: 0111 + 1 -> 1000。
- 结果:-(-8) 的计算结果是 1000,即 -8。失败了,因为 +8 不在 [-8, 7] 的范围内。
- 示例2: 8位2的补码系统 (常见的 signed char)
- 范围: -128 到 +127。
- 最小的负数是 -128,其二进制表示是 10000000。
- 让我们对 -128 (10000000) 取反:
- 按位取反: 10000000 -> 01111111。
- 加1: 01111111 + 1 -> 10000000。
- 结果:-(-128) 的计算结果是 10000000,即 -128。同样失败了,因为 +128 超出了 [-128, 127] 的范围。
- 最重要的边界情况: 这个最小负数是2的补码系统中最经典的边界情况。在编写代码时,对一个变量 x 执行 -x 操作,如果 x 恰好是该数据类型能表示的最小负数,结果将不是预期的正数,而是一个溢出(在C语言等语言中,这是未定义行为,但实际表现往往是数值不变)。
- 误认为所有数都能成功取反: 这是一个常见的误解。必须时刻记住数据类型的表示范围,任何操作的结果都不能超出这个范围,否则就会发生溢出。
- 绝对值函数 abs() 的陷阱: 同样,对最小负数取绝对值 abs(INT_MIN) 也会导致同样的问题,因为其结果 +INT_MAX+1 无法表示。
本段通过标题和表格,揭示了2的补码表示法的一个重要特性:表示范围的不对称性,以及由此导致的最负数无法被成功取反的边界情况。这个“取反失败”的现象本质上是一种算术溢出。
这一部分的目的是深入探讨2的补码的一个关键细节和潜在陷阱。在享受2的补码带来的算术便利性的同时,程序员和系统设计者必须了解并正确处理其边界行为。这对于编写健壮、无错的底层代码至关重要。
回到那个环形的里程表/钟表的模型。范围是-4到+3。
- 0 在12点位置。
- 1, 2, 3 分别在1点、2点、3点位置。
- -1, -2, -3, -4 分别在11点、10点、9点、8点位置(假设钟表只有8个刻度)。
- 取反操作可以想象成“以0为中心点,找到环对面位置的数”。
- 1 (1点) 的对面是 -1 (不对,应该是-3或-4附近,这个模型需要修正)。
- 更好的心智模型: “取反”是计算“从0点出发,走多少步能回到0”。从0走 x 步,再走 -x 步,应该回到0。
- 例如,从0 (000) 走3步到 3 (011)。-3 是 101。我们计算 011 + 101。结果是 (1)000,忽略进位就是 000。正确。
- 现在看 -4 (100)。从0走 -4 步到了 100。它的相反数也计算为 100。我们计算 100 + 100,结果是 (1)000,忽略进位是 000。在这个模运算的环上, -4 加上 -4 居然回到了0!这说明在这个8个数的环上,-4 这个点很特殊,它自己是自己的“加法逆元”,就像实数中只有0是自己的加法逆元一样。这正是问题的根源。
想象你在一条很短的直尺上测量,尺子刻度是从-4到+3。你有一个神奇的“反转棒”,把一个正数 x 变成 -x,把负数 -y 变成 y。
- 你用“反转棒”碰了一下 +3,它变成了 -3。
- 你用“反转棒”碰了一下 -2,它变成了 +2。
- 你用“反-转棒”碰了一下 -4,但什么也没发生!尺子的+4那个位置是空的,棒子找不到可以变换过去的地方,所以-4就留在了原地。这个“反转棒”在这个点上“失灵”了。
22.2. 使用二进制加法算法
📜 [原文4]
在 2 的补码中,二进制加法算法总是有效的(除非发生溢出)!
这一部分阐述了2的补码表示法最核心的优势:它极大地简化了计算机的算术运算。
- 核心论点: “在 2 的补码中,二进制加法算法总是有效的(除非发生溢出)!”。这句话的含义是,无论两个数字是正数还是负数,你都可以将它们的2的补码形式直接相加,就像它们是无符号数一样。你不需要预先检查它们的符号,也不需要根据符号来决定是做加法还是减法。得到的二进制结果,如果把它解释为2的补码,就是正确的算术和。这使得硬件设计(即算术逻辑单元ALU)可以非常简单和高效。
- “除非发生溢出”: 这是一个至关重要的限定条件。溢出(Overflow)指的是计算结果超出了当前数据类型所能表示的范围。例如,在4位2的补码(范围-8到+7)中,计算 5 + 5 = 10。10 无法在4位2的补码中表示,因此发生了溢出。在这种情况下,虽然二进制加法算法本身仍然按照规则执行,但最终得到的二进制结果不再代表正确的算术和。
- 公式与示例分析:
- 公式部分展示了一个具体的例子:计算 5 + (-3)。
- 在4位2的补码系统中:
- +5 的表示是 0101。
- +3 的表示是 0011。要得到 -3,我们对 0011 按位取反得到 1100,再加1得到 1101。所以 -3 的表示是 1101。
- 二进制加法:
- 加法过程:
- 最右边(最低位): 1 + 1 = 10 (二进制),所以结果位是 0,向左进位 1。
- 第二位: 1 (进位) + 0 + 0 = 1。结果位是 1,无进位。
- 第三位: 1 + 1 = 10 (二进制)。结果位是 0,向左进位 1。
- 第四位(最高位): 1 (进位) + 0 + 1 = 10 (二进制)。结果位是 0,向左进位 1。
- 结果解读: 最终的4位结果是 0010。在2的补码中,0010 代表 +2。这与我们预期的数学结果 5 + (-3) = 2 完全一致。
- 最高进位: 注意,从最高位产生了一个进位 1(在 (1)0010 中用括号表示)。在2的补码加法中,这个从最高位溢出的进位通常被丢弃。
- 示例1: 负数 + 负数 (4位系统)
- 计算 -2 + (-3)。预期结果是 -5。
- -2 的2的补码: +2 是 0010 -> 取反 1101 -> 加1 1110。
- -3 的2的补码: +3 是 0011 -> 取反 1100 -> 加1 1101。
- 加法:
```
111 (进位)
1110 (-2)
+ 1101 (-3)
-------
(1)1011 (-5)
```
- 结果 1011。这是一个负数。我们来验证它的值:减1 -> 1010 -> 取反 0101 (即5)。所以 1011 确实是 -5。计算正确。
- 示例2: 导致溢出的加法 (4位系统)
- 计算 6 + 7。预期结果是 13。但在4位2的补码(范围-8到+7)中,13 无法表示。
- 6 的2的补码是 0110。
- 7 的2的补码是 0111。
- 加法:
```
111 (进位)
0110 (6)
+ 0111 (7)
-------
1101 (-3)
```
- 结果 1101,在2的补码中代表 -3。这显然不等于 13。这里就发生了溢出。两个正数相加,结果却成了一个负数,这是溢出的典型特征。
- 忽略溢出: 最常见的错误是假设加法总是正确的,而忘记检查溢出。在实际编程中,未处理的整数溢出是许多安全漏洞和程序错误的根源。
- 处理最高位进位: 在2的补码加法中,从最高有效位(MSB)产生的进位(carry-out)本身并不直接表示溢出,它应该被丢弃。溢出的判断有专门的规则(后面会讲)。
- 混淆加法和减法: 2的补码的优雅之处在于,减法 A - B 可以通过计算 A + (-B) 来实现。而计算 -B 就是对 B 的二进制表示执行“按位取反再加1”的操作。这样,减法器硬件可以被加法器和一些简单的逻辑门替代,大大节省了成本。
本段强调了2的补码表示法的核心优点:它允许计算机使用单一、简单的二进制加法算法来处理所有整数的加法(和减法),无需关心数字的符号。这个特性极大地简化了硬件设计。同时,本段也引入了算术溢出的概念,即当计算结果超出表示范围时,这个简便的算法会得出错误答案。
本节的目的是解释“为什么计算机科学家和工程师如此钟爱2的补码?”。答案就是:为了算术运算的“简单”和“统一”。这个看似微小的表示法选择,是构建高效、快速的中央处理器(CPU)的基石之一。
再次使用环形里程表的模型。加法就是在这个环上顺时针旋转,减法就是逆时针旋转。
- 5 + (-3) 可以看作:从0点顺时针走5步,然后逆时针走3步。最终停在+2的位置。
- 二进制加法算法的巧妙之处在于,它把“逆时针走3步”等价于“顺时针走 最大值 - 3 步”。在这个8个刻度的环上,逆时针3步和顺时针5步会到达同一个点。而-3的2的补码 101,如果看作无符号数,恰好就是5。所以 5 + (-3) 就变成了在模8的环上计算 5 + 5,5+5=10,10 mod 8 = 2。结果正确!
- 这个模型也很好地解释了溢出。6 + 7 在8位系统(-8到+7)上,是从0顺时针走6步,再顺时针走7步。总共走了13步,在一个只有8个刻度的钟表上,13 mod 8 = 5,不对,这里应该用16个刻度的钟表(-8到+7)。6+7 = 13,在模16的意义下,13就是13,但这个值在我们的有符号范围里不存在。6 (0110) + 7 (0111) = 13 (1101),而 1101 被我们定义为了 -3。所以,你以为你在向前走,但因为走得太远“绕回了”环的负数区域。
想象你在一条生产线上组装玩具。
- 使用符号与幅度表示法:你面前有两箱零件,你需要先检查箱子上的标签是“+”还是“-”。如果都是“+”,你用加法说明书。如果都是“-”,你也用加法说明书但最后要在成品上贴个“-”标签。如果一个“+”一个“-”,你得拿出另一本减法说明书,还要比较哪个箱子的零件多,来决定最后贴什么标签。非常麻烦。
- 使用2的补码表示法:所有零件箱都用同一种编码。你只有一本说明书,就是“加法”。无论来什么箱子,你只管把它们倒在一起,按照加法说明书组装。组装完的成品自动就是正确的(除非零件太多装不下了,这就是溢出)。这条生产线简单、高效、出错少。
32.3. 使用二进制加法算法
📜 [原文5]
当发生溢出时,结果将差 $2^{\text{字长}}$
这句话是对2的补码算术中溢出现象的一个精确定量描述。它告诉我们,当溢出发生时,错误的计算结果和正确的数学结果之间存在一个固定的关系。
- 核心含义: 如果你用一个 k 位的2的补码系统进行加法运算,发生了溢出,那么计算机得到的那个不正确的答案(我们称之为CompuResult)与本应得到的正确数学答案(我们称之为MathResult)之间的差值,正好是 $2^k$ (其中 k 是字长,即二进制的位数)。
- 数学关系:
- CompuResult = MathResult - 2^k (如果 MathResult 太大,发生了正向溢出)
- CompuResult = MathResult + 2^k (如果 MathResult 太小,发生了负向溢出)
- 这两种情况可以统一表示为:CompuResult ≡ MathResult (mod 2^k)。这读作“计算机结果与数学结果在模 $2^k$ 的意义下同余”。模运算(Modulo Operation)是理解计算机整数算术的关键。计算机的所有整数运算,无论是无符号还是2的补码,本质上都是在模 $2^k$ 的环上进行的。
- 为什么是 $2^k$?
一个 k 位的二进制数可以表示 $2^k$ 个不同的状态。想象一个 k 位的计数器,从 00...0 开始计数,每加1,状态变化一次,直到 11...1。如果再加1,会发生什么?
11...1 + 1 = (1)00...0。
最高位产生了一个进位 1,而计数器的 k 位都归零了。这个溢出的进位 1 代表的值就是 $2^k$。由于计算机(通常)只保留 k 位结果,这个进位被丢弃了,相当于整个结果被减去了 $2^k$。这就是“差 $2^{\text{字长}}$”的根本原因。
- 示例1: 正向溢出 (4位系统)
- 字长 k = 4。所以 $2^k = 2^4 = 16$。
- 计算 6 + 7。
- MathResult = 13。
- 计算机计算:0110 (6) + 0111 (7) = 1101。
- CompuResult = 1101 (在2的补码中是-3)。
- 验证关系:CompuResult 是否等于 MathResult - 2^k?
- -3 = 13 - 16。
- 关系成立!计算机得到的结果 -3 确实比正确答案 13 小了16。
- 示例2: 负向溢出 (4位系统)
- 字长 k = 4。所以 $2^k = 2^4 = 16$。
- 计算 -5 + (-6)。
- MathResult = -11。这个值超出了4位2的补码的范围 [-8, 7]。
- -5 的表示是 1011。
- -6 的表示是 1010。
- 计算机计算:1011 (-5) + 1010 (-6) = (1)0101。丢弃进位后结果是 0101。
- CompuResult = 0101 (在2的补码中是+5)。
- 验证关系:CompuResult 是否等于 MathResult + 2^k?
- 5 = -11 + 16。
- 关系成立!计算机得到的结果 +5 确实比正确答案 -11 大了16。
- 字长的意义: k 是字长,不是表示范围内的数字个数。对于8位系统,k=8, $2^k = 256$;对于32位系统,k=32, $2^k$ 是一个非常大的数。
- 正负溢出的混淆: 正向溢出(两个正数相加得到负数)意味着结果“环绕”到了负数区,实际值比正确值小了 $2^k$。负向溢出(两个负数相加得到正数)意味着结果“环绕”到了正数区,实际值比正确值大了 $2^k$。
- 正负数相加: 一个正数和一个负数相加,结果的绝对值一定小于其中绝对值较大的那个数。因此,它们的和一定在表示范围内,永远不会发生溢出。
本句精辟地总结了2的补码算术溢出的后果:计算出的错误结果与真实的数学结果精确地相差 $2^k$(其中k为字长)。这揭示了计算机整数算术的本质是模运算。
这一知识点不仅帮助我们理解溢出的本质,在某些高级编程技巧和底层算法中甚至可以被利用。例如,一些密码学或哈希算法会故意利用整数运算的环绕特性。同时,它也为我们设计溢出检测逻辑提供了理论基础。
想象你的汽车里程表只有4位,最大能显示9999公里。它就是一个模 $10^4$ (10000) 的系统。
- 你的车已经开了9998公里。你再开3公里。
- MathResult = 9998 + 3 = 10001公里。
- 里程表的变化是:9998 -> 9999 -> 0000 -> 0001。
- CompuResult (里程表读数) = 1公里。
- CompuResult = MathResult - $10^4$。即 1 = 10001 - 10000。
- 这个“差 $10^4$”就和计算机里“差 $2^k$”是完全相同的道理。里程表“溢出”了,从最大值绕回了最小值。
想象你在玩一个圆盘形的棋盘游戏,棋盘有16个格子,编号从-8到+7。
- 你现在在+6的位置,你的骰子掷出了+7。
- 数学上你应该前进7步,到达+13。但棋盘上没有+13。
- 你实际的移动是:从+6 -> +7 -> (越过边界) -> -8 -> -7 -> -6 -> -5 -> -4 -> -3。你最终停在了-3的格子上。
- 你的最终位置(-3)和你本应到达的位置(+13)之间,正好隔了16个格子,也就是整个棋盘的大小 ($2^4$)。你因为走得太远,“掉进了”棋盘的另一端。
33. 2 的补码的特殊之处
13.1. 模运算与溢出的关联
📜 [原文6]
- 与无符号数类似,当使用 BAA 进行加法时,结果在 $\bmod 2^{\mathrm{k}}$ 下是正确的( $k$ 是字长)
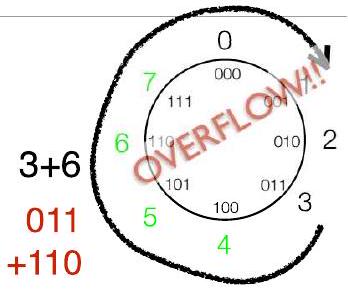
- 无论是无符号还是 2 的 补码形式,都将落在模 $2^{k}$ 正确的值上,但如果不在风车上则实际值不正确
- 思考模运算(例如,$\bmod 8$)
- 如果我们选择“无符号” $\bmod 8 = (0,1,2,3,4,5,6,7)$
- $3+6 \bmod 8=1$(即 $\text{余数}(9/8)$)
- $3-6 \bmod 8=5$
这一部分深入探讨了计算机算术的核心——模运算,并将其与2的补码、无符号数以及溢出联系起来。这里的“风车”图是一种形象化的表示,用来展示数字在模运算下的循环特性。
- BAA - 二进制加法算法: BAA 是 “Binary Addition Algorithm” 的缩写,就是我们之前讨论的,像做小学加法一样,逐位相加并处理进位的算法。
- 核心论点1: “与无符号数类似,当使用 BAA 进行加法时,结果在 $\bmod 2^{\mathrm{k}}$ 下是正确的”。
- 这句话是统一了无符号数和2的补码的算术行为。它指出,无论你把一串二进制位看作无符号数还是2的补码数,用标准的二进制加法得到的结果,在模运算的意义下都是对的。
- 例如,0110 (6) + 0111 (7) = 1101。
- 在无符号视角下:6 + 7 = 13。1101的无符号值就是13。正确。
- 在2的补码视角下:6 + 7 = 13。但1101的2的补码值是-3。虽然-3不等于13,但是 $ -3 \equiv 13 \pmod{16}$ (因为 $-3 = 13 - 16$)。所以“在模 $2^4$ 下是正确的”。
- 核心论点2: “无论是无符号还是 2 的 补码形式,都将落在模 $2^{k}$ 正确的值上,但如果不在风车上则实际值不正确”。
- “风车”或环形图代表了特定数据类型所能表示的合法数值集合。
- 对于3位无符号数,这个集合是 {0, 1, 2, 3, 4, 5, 6, 7}。
- 对于3位2的补码数,这个集合是 {-4, -3, -2, -1, 0, 1, 2, 3}。
- BAA 计算出的二进制结果,总会对应这个环上的一个点。这个点在模运算意义下是正确的。
- 然而,数学上的正确答案可能不在这个环上(例如,3位系统计算 5+5=10,10 就不在 {0..7} 或 {-4..3} 的环上)。这时,虽然计算机给出的结果(10 mod 8 = 2)在环上有一个位置,但它不等于数学上的真实值10。这就是“实际值不正确”,也就是我们所说的“溢出”。
- 无符号模运算示例:
- 这里以 $\bmod 8$ 为例,对应3位系统 ($2^3 = 8$)。
- 无符号数的集合是 {0, 1, 2, 3, 4, 5, 6, 7}。
- 3 + 6 = 9。数学结果是9。9不在集合中,发生溢出。计算机的结果是 9 mod 8 = 1。
- 二进制计算: 011 (3) + 110 (6) = (1)001。丢弃进位后是 001,即1。
- 3 - 6 = -3。数学结果是-3。-3不在集合中,发生溢出(无符号数不能表示负数)。计算机的结果是多少呢?在模8的环上,-3 和 5 是等价的(因为 $-3+8=5$)。所以 3 - 6 ≡ 5 (mod 8)。
- 二进制计算: 3 - 6 等价于 3 + (-6)。在3位2的补码中,-6是010。011 (3) + 010 (-6, 咦这里-6应该是1010,不对,3位系统里-6不存在)。应该这样计算:011 - 110。需要借位,很复杂。但如果我们用模运算心智模型,就很容易理解结果是5。
- 示例1: 4位系统 (k=4, mod 16)
- 计算 10 + 10。
- 无符号视角:
- MathResult = 20。
- 二进制: 1010 (10) + 1010 (10) = (1)0100。
- CompuResult = 0100 (4)。
- 验证:$4 \equiv 20 \pmod{16}$ (因为 $4 = 20 - 16$)。模意义下正确,但发生溢出。
- 2的补码视角:
- 1010 代表-6。所以计算的是 -6 + (-6)。
- MathResult = -12。
- CompuResult = 0100 (+4)。
- 验证:$4 \equiv -12 \pmod{16}$ (因为 $4 = -12 + 16$)。模意义下正确,但发生溢出。
- 示例2: 理解 3 - 6 mod 8 = 5
- 想象一个8个格子的钟表,格子编号0到7。
- 你现在在格子3。
- 减6,就是逆时针走6步。
- 从3 -> 2 -> 1 -> 0 -> 7 -> 6 -> 5。最终停在格子5。
- 所以 3 - 6 在这个模8的系统里,结果是5。
- 混淆模运算的正确性和实际值的正确性: BAA保证了模运算的正确性,但不保证实际值的正确性。只有在不发生溢出(即数学结果仍在表示范围内)时,CompuResult 才等于 MathResult。
- 对负数的模运算: a mod n 的标准定义是 a - n floor(a/n)。对于负数,例如 -3 mod 8,-3 - 8 floor(-3/8) = -3 - 8 * (-1) = 5。所以 -3 \equiv 5 \pmod{8}。
- 减法即加法: 计算机通过“加上一个负数”来实现减法。A - B 变成 A + (2's complement of B)。这个操作的美妙之处在于它完全符合模运算。
本段将计算机的整数加法统一到了模运算的框架下。无论是无符号数还是2的补码,硬件执行的都是相同的二进制加法算法(BAA),其结果在 $\bmod 2^k$ 意义下总是正确的。而我们通常所说的“溢出”,指的就是数学结果落在了表示范围(“风车”)之外,导致计算机给出的(在模意义下正确的)值与实际数学值不符的情况。
本节的目的是提供一个更高层次的、更根本的视角来理解计算机的整数算术。将所有运算都看作是在一个有限大小的环上进行的模运算,可以帮助我们统一理解无符号数、2的补码、加法、减法和溢出等看似孤立的概念。
“风车”或“钟表”模型是理解本节最核心的心智模型。
- k: 钟表上有多少个刻度 ($2^k$)。
- BAA: 拨动指针的规则(顺时针或逆时针)。
- 无符号/2的补码: 给这些刻度赋予不同含义的标签。无符号是 {0, 1, ..., $2^k-1$}。2的补码是 {$-2^{k-1}$, ..., 0, ..., $2^{k-1}-1$}。
- 运算: 无论你怎么给刻度贴标签,从一个点拨动n格,到达的物理位置是固定的。这就是“模意义下正确”。
- 溢出: 你想让指针指向一个叫“13点”的位置,但你的钟表上根本没有这个标签。指针实际停在了一个有标签的位置(比如“1点”,如果钟表是12小时制),但这个标签不是你想要的“13点”。
想象你在一条环形跑道上跑步,跑道一圈长1600米。
- k=4 (假设跑道长16米),mod 16。
- 你从起点出发,跑了10米,又跑了10米。总共跑了20米。
- 你的物理位置在:跑完一圈(16米)后,又向前跑了4米。所以你停在距离起点4米的地方。
- 无符号视角:你跑了20米,但位置在4米处。20 mod 16 = 4。
- 2的补码视角:这条跑道的另一半被标记为负距离。比如10米处可能被标记为“-6米处”。你从“-6米处”出发,又“前进”(加上)“-6米”。结果你停在了“+4米处”。-6 + (-6) = -12,而 -12 \equiv 4 \pmod{16}。
- 无论你怎么解释这些位置的标签,你跑20米最终停在4米处这个物理事实是不变的。
23.2. 补码环形表示(风车)
📜 [原文7]
- 但也可以选择“2 的 补码” $\bmod 8 = (-4,-3,-2,-1,0,1,2,3)$
- 6(即 110)将变为 -2
- $3+(-2) \bmod 8 = 3-2 \bmod 8 = 1$
- $3-(-2) \bmod 8 = 3+2 \bmod 8 = -3$
011
+110
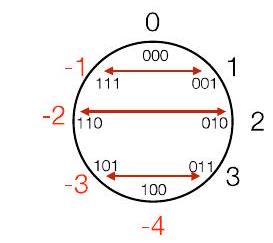
这部分继续深化模运算与2的补码的关系,通过一个具体的例子展示了2的补码如何将减法运算转化为加法运算,并自然地落在正确的模结果上。
- 切换视角: 前面我们讨论了mod 8下的无符号数集合 {0,1,2,3,4,5,6,7}。现在,我们把同样的二进制模式(000 到 111)用2的补码的规则来解释。这就得到了新的数值集合:“2 的 补码” $\bmod 8 = (-4,-3,-2,-1,0,1,2,3)$。
- 重新解释二进制模式:
- 在无符号视角下,110 是 6。
- 在2的补码视角下,110 是 -2。
- 这是一个关键的转变:“6(即 110)将变为 -2”。这里的“6”指的是无符号值,而“-2”是它在2的补码下的等价值。同一个二进制模式 110,有了两种不同的解读。
- 用2的补码进行运算: 现在,我们重新计算之前那个 3-6 的例子,但这次把所有数字都看作是2的补码。
- 3 - 6 变成了 3 + (-6)。
- 在3位2的补码里,-6是无法表示的(范围是-4到+3)。所以原文例子做了一个 slight modification,它计算的是 3+(-2),而不是 3+(-6)。这是为了让所有操作数都在3位2的补码表示范围内。
- 让我们来分析原文的计算:3+(-2)。
- 3 的二进制是 011。
- -2 的二进制是 110。
- 二进制加法: 011 + 110
- 结果是 001,即 +1。
- 这与数学计算 3 + (-2) = 1 完全一致。
- 所以,$3+(-2) \bmod 8 = 1$。
- 减法变加法: 现在看减法 3 - (-2)。
- 这等价于 3 + 2。
- 3 是 011,2 是 010。
- 二进制加法: 011 + 010 = 101。
- 101 在2的补码里是什么?它是负数。减1得100,取反得011(3)。所以 101 是 -3。
- 数学计算 3 + 2 = 5。但 5 无法在3位2的补码中表示,发生了溢出。
- 计算机给出的结果是 -3。我们来验证一下模运算关系:$-3 \equiv 5 \pmod 8$ (因为 $-3 = 5 - 8$)。
- 所以 $3-(-2) \bmod 8 = 3+2 \bmod 8 = 5 \bmod 8 = -3$。这里的 $=-3$ 是指在2的补码表示下的结果。
- $3+(-2) \bmod 8 = 3-2 \bmod 8 = 1$
- 3+(-2): 这是我们想做的数学运算。
- mod 8: 表示我们是在一个能表示8个状态的系统(3位系统)中进行运算。
- = 3-2: 这是等价的数学运算。
- = 1: 这是最终的数学结果。由于 1 在3位2的补码的表示范围 [-4, 3] 内,所以计算机得到的结果和数学结果一致,没有溢出。
- $3-(-2) \bmod 8 = 3+2 \bmod 8 = -3$
- 3-(-2): 我们想做的数学运算。
- = 3+2: 等价的数学运算,结果是 5。
- mod 8: 在3位系统中运算。
- = -3: 这是计算机给出的结果 (101)。
- 这里发生了溢出,因为数学结果 5 不在表示范围 [-4, 3] 内。计算机结果 -3 和数学结果 5 满足模8同余关系 ($-3 \equiv 5 \pmod 8$)。
- 示例1: 4位2的补码系统 (mod 16)
- 计算 -7 - 3。这等于 -7 + (-3)。
- MathResult = -10。
- -7 的2的补码: +7是0111 -> 取反1000 -> 加11001。
- -3 的2的补码: +3是0011 -> 取反1100 -> 加11101。
- 二进制加法:
```
1 1 (进位)
1001 (-7)
+ 1101 (-3)
--------
(1)0110 (+6)
```
- CompuResult = 0110 (+6)。
- 发生了溢出,因为-10不在[-8, 7]范围内。
- 验证: $6 \equiv -10 \pmod{16}$ (因为 $6 = -10 + 16$)。
- 示例2: 4位2的补码系统 (mod 16)
- 计算 5 - (-4)。这等于 5 + 4。
- MathResult = 9。
- 5 的2的补码是 0101。
- -4 的2的补码是 1100。
- 二进制加法:
```
0101 (5)
+ 1100 (-4)
--------
0001 (1)
```
等等,上面例子是 5-(-4),我算成了 5+(-4)。重来。
- 5 - (-4) 等于 5 + 4。
- 4 的2的补码是 0100。
- 二进制加法:
```
0101 (5)
+ 0100 (4)
--------
1001 (-7)
```
- MathResult = 9。
- CompuResult = 1001 (-7)。
- 发生了溢出,因为9不在[-8, 7]范围内。
- 验证: $-7 \equiv 9 \pmod{16}$ (因为 $-7 = 9 - 16$)。
- 在哪个系统里说话: 一定要分清当前讨论的是无符号系统还是2的补码系统。同一个二进制模式,如110,在不同系统里代表完全不同的值(6 vs -2)。
- 忘记溢出: 即使是负数加法也可能溢出。只要数学结果超出了表示范围,就是溢出。
- -3的解读: 在 3+2 mod 8 = -3 中,-3 不是一个随意的数字,它是 101 这个二进制模式在3位2的补码系统下的标准解释。
本段通过具体示例,展示了2的补码表示法如何将所有加减法都统一为简单的二进制加法。即使发生溢出,其结果在模运算的意义下仍然是正确的。这再次证明了2的补码在简化计算机硬件设计上的巨大优势。
目的是通过一个 hands-on 的例子,让读者亲身体验2的补码的算术过程,并直观地看到溢出是如何发生的,以及溢出后的结果与模运算之间的关系。这是对前面理论部分的一个实践验证。
继续使用环形钟表模型(刻度为-4到+3)。
- 3 + (-2): 从+3的位置,逆时针走2步。+3 -> +2 -> +1。停在+1。正确。
- 3 - (-2) (即3+2): 从+3的位置,顺时针走2步。+3 -> (越过边界) -> -4 -> -3。停在-3。发生了溢出。数学结果是5,但钟表上没有5这个刻度,你“绕了一圈”到了-3的位置。
想象你是一个会计,但你只有一个非常奇怪的计算器。这个计算器做减法的方式是加上一个“魔法数字”。
- 要计算 3 - 2,你输入 3,然后加上 2 的“魔法形式” (-2的2的补码 110)。计算器显示 1。很棒。
- 要计算 3 - (-2),也就是 3+2。你输入 3,加上 2。计算器突然警报灯一闪(溢出了),然后显示了一个奇怪的数字 -3。
- 你发现这个计算器就像一个循环的尺子,当你想测量的长度超出了尺子的最大正刻度时,它会从负刻度的末端开始重新计数。
33.3. C语言中的补码示例
📜 [原文8]
```
int main() {
int x = 47;
int y=-50;
unsigned int z = 50;
printf("%d %d %uln", x, y, z);
}
```
你(无意中)在哪里使用过 2 的补码?
```
int main() {
int x = 47;
int y=-50;
unsigned int z = 50;
printf("%d %d %uln", x, y, z);
}
- The computer represents
- x and y as signed 2 's complement
- $z$ as an unsigned
- C Demo: https://onlinegdb.com/49zlpDA9P8
- Note:
- $0 \times F$ (in Hex) is $15=1111$ in (unsigned) binary
- $0 \times 8$ (in Hex) is $8=1000$ in (unsigned) binary
- $2^{32}=4,294,967,296$ and $2^{31}=2,147,483,648$
```
这部分将前面讨论的理论知识与实际的编程语言(C语言)联系起来,说明我们日常编程中其实一直在不知不觉地使用2的补码。
- C语言中的数据类型:
- 在C语言中,当我们声明一个int类型的变量时,它默认是signed int,即有符号整数。现代计算机体系结构(如x86, ARM)几乎无一例外地使用2的补码来表示有符号整数。
- 因此,int x = 47; 和 int y = -50; 这两行代码,编译器和CPU在底层就是用2的补码来存储和操作x和y的。
- 当我们声明unsigned int z = 50;时,我们明确告诉编译器,z是一个无符号整数。它的底层表示就是标准的二进制。
- printf格式说明符:
- printf函数通过格式说明符来决定如何解释内存中的二进制数据。
- %d:告诉printf把对应的参数(一个int)当作一个有符号的十进制整数来解释和打印。它假定内存中的数据是2的补码形式。
- %u:告诉printf把对应的参数(一个unsigned int)当作一个无符号的十进制整数来解释和打印。
- (注意:原文中的 %uln 可能是笔误,应该是 %u\n,\n是换行符)。
- 核心思想: “你(无意中)在哪里使用过 2 的补码?” 答案是:每当你使用int、short、long、char(通常默认为signed)等有符号整数类型时,你就在使用2的补码。这是编程语言和底层硬件之间的一个约定。你不需要手动进行“取反加一”的操作,编译器和CPU已经为你做好了这一切。
- 笔记解释:
- x and y as signed 2's complement: 确认了x和y是用2的补码表示。
- z as an unsigned: 确认了z是用无符号二进制表示。
- C Demo链接: 提供了一个在线的C语言编译器环境,可以运行这段代码来验证输出。
- Hex (十六进制) 注释: 这是为了说明二进制、十六进制和十进制之间的关系,并为可能涉及的更大数字做铺垫。0xF (十六进制的F) 等于十进制的15,二进制的1111。0x8等于8,二进制的1000。
- 2^32和2^31: 这些是32位系统中常见的边界值。一个32位的无符号整数范围是 0 到 $2^{32}-1$。一个32位的有符号整数(2的补码)范围是 $-2^{31}$ 到 $2^{31}-1$。这些数值定义了unsigned int和int的取值范围。
- 示例1: 8位系统下的 char
- 假设我们有 signed char y = -50;。
- 一个signed char是8位的。
- +50 的8位二进制是 00110010。
- 要得到 -50 的2的补码:
- 取反: 11001101
- 加1: 11001110
- 所以,在内存中,变量y的8个比特就是11001110。当printf("%d", y);执行时,printf会读取这8个比特,按照2的补码规则把它解释回-50并打印出来。
- 示例2: 强制类型转换的危险
- 考虑以下代码:
```c
int y = -50;
unsigned int z;
z = y; // 把一个负数赋给无符号整数
printf("y = %d, z = %u\n", y, z);
```
- 在32位系统中,-50的2的补码是 11111111 11111111 11111111 11001110。
- 当 z = y; 执行时,底层的32个比特被原封不动地复制给了z。
- 现在,printf被要求用 %u (无符号) 来解释z的这堆比特。
- 1111...11001110 作为一个无符号数是一个非常大的正数,它等于 $2^{32} - 50 = 4294967246$。
- 所以,程序的输出会是 y = -50, z = 4294967246。
- 这个例子极好地说明了同一串二进制位在不同解释(%d vs %u)下,代表的数值是天差地别的。
- 有符号与无符号混用: 在C语言中,混合使用signed和unsigned整数进行运算,可能会导致非预期的结果。C语言有一套复杂的“整数提升”和“寻常算术转换”规则。一个常见的陷阱是: if (-1 < 0u),这个表达式的结果是false!因为 -1 会被转换成一个非常大的unsigned int,它比0u要大。
- printf格式说明符错误: 如果为int y = -50; 使用 %u 来打印,printf("%u", y);,就会得到那个巨大的正数,而不是-50。这是因为你命令printf用错误的“镜头”去看待内存中的数据。
- 平台依赖性: 虽然标准建议int至少是16位,但在现代几乎所有平台上,int都是32位的。char的符号性(signed or unsigned)在C标准中是实现定义的(implementation-defined),不过在x86等主流平台上通常默认为signed。
本节通过一个简单的C语言代码示例,将抽象的2的补码理论与我们日常的编程实践联系起来。它揭示了一个事实:作为程序员,我们一直在使用2的补码,尽管这个过程被编译器和硬件“隐藏”了。理解这一点有助于我们更深刻地理解数据类型、类型转换和潜在的编程陷阱。
这一部分的目的是“接地气”,展示理论知识在现实世界中的应用。它弥合了理论与实践之间的鸿沟,让学习者明白,前面所学的关于二进制表示法的知识,并不是屠龙之技,而是理解和编写高质量代码所必需的内功。
- int, unsigned int 就像是不同颜色的眼镜。
- 内存中的二进制数据就像是一幅画。
- 当你戴上 int 这副“2的补码眼镜”(通过%d),你看到的是有正有负的正常世界。
- 当你换上 unsigned int 这副“无符号眼镜”(通过%u),你看到的世界里没有负数,原本是负数的地方变成了一些非常刺眼、巨大的正数。
- 画本身(内存中的比特)没有变,变的是你看待它的方式(解释规则)。
想象你去银行存钱。
- 你存了47元,银行在你的账户(变量x)的“正数账本”上记了一笔。
- 你朋友欠了银行50元,银行在他的账户(变量y)的“负数账本”上记了一笔。这个“负数账本”用的就是2的补码记账法。
- 另一个人参加一个积分活动,获得了50积分,银行在他的账户(变量z)的“积分账本”上记了一笔。这个“积分账本”只能记正数,用的就是无符号记账法。
- 当你去查询余额时,柜员(printf)会根据你要查的是“存款账户”(%d)还是“积分账户”(%u),拿出对应的账本来看,然后告诉你正确的数字。如果你让柜员用看“积分账户”的方法去查你朋友的“负数账户”,他会懵掉,然后报出一个莫名其妙的巨大正数。
43.4. “翻转位+1”的直观解释
📜 [原文9]
负值正好在对面
2 的补码

所有位翻转的值比正好在对面的值顺时针少 1 刻度
这部分试图通过“风车”或“钟表”图,给2的补码取反操作(按位取反再加1)一个直观的几何解释。
- “负值正好在对面”: 这句话设定了一个理想的、对称的期望。在一个圆环上,我们很自然地会认为一个数 x 的相反数 -x 应该在圆环上与 x 处于“正对面”的位置。例如,在钟表上,3点钟的正对面是9点钟。
- “2的补码”图: 这张图展示了3位2的补码的环形排列。
- 000 (0) 在顶部。
- 顺时针方向是正数: 001 (1), 010 (2), 011 (3)。
- 逆时针方向是负数: 111 (-1), 110 (-2), 101 (-3), 100 (-4)。
- 注意 +3 和 -4 是相邻的,这体现了模运算的环绕特性。
- 核心观察: “所有位翻转的值比正好在对面的值顺时针少 1 刻度”。 这是本段最关键的洞见。让我们来验证一下:
- 以 +1 (001) 为例。
- 它的“正对面”是谁?在8个刻度的环上,从 +1 (位置1) 走半圈(4步),会到达 -3 (位置5)。所以 +1 的“几何对面”是 -3。
- 对 +1 (001) 进行“按位取反”操作,得到 110。110 在图上是 -2。
- 比较一下,“按位取反”得到的值 -2 和“几何对面”的值 -3,是不是正好差了1个顺时针刻度?是的,从 -3 顺时针走一步就是 -2。
- 再以 +3 (011) 为例。
- 它的“几何对面”是 -1。
- 对 +3 (011) 进行“按位取反”操作,得到 100。100 在图上是 -4。
- 比较一下,“按位取反”得到的值 -4 和“几何对面”的值 -1。它们不符合“少1刻度”的规律。
- 让我们换一种理解方式: 可能“正对面”的定义不是几何上的,而是数值上的。 -x 是 x 的相反数。
- 我们想找到 -x 的位置。
- 2的补码规则是 -x = NOT(x) + 1。
- 这个公式可以改写为 NOT(x) = -x - 1。
- NOT(x) 就是“所有位翻转的值”。
- -x 就是 x 的相反数。
- 所以,这句话的精确意思是:一个数x按位取反后的值,等于x的相反数再减1。
- 在环形图上,“减1”就等价于“逆时针走1步”。
- 所以,要找到 NOT(x) 在哪,你先找到 x 的相反数 -x,然后从 -x 的位置再逆时针走一步。
- 这与原文的“顺时针少1刻度”是相反的方向。原文可能存在一点笔误或理解偏差。我们以 NOT(x) = -x - 1 为准。
- 验证: 找 NOT(1)。1 是 001。NOT(1) 是 110 (即-2)。根据公式,它应该等于 -1 - 1 = -2。正确!
- 验证: 找 NOT(3)。3 是 011。NOT(3) 是 100 (即-4)。根据公式,它应该等于 -3 - 1 = -4。正确!
- 最终解释: 2的补码的取反操作 -x = NOT(x) + 1,提供了一个几何上的直观操作:要找到一个数 x 的相反数 -x,你可以先将 x 的所有位翻转得到 NOT(x),然后在环形图上从 NOT(x) 的位置再顺时针走一步。
- 示例1: 求 -2 (4位系统)
- x = 2,二进制为 0010。
- 步骤1 (翻转所有位): NOT(2) 是 1101。在2的补码中,1101 是 -3。
- 步骤2 (加1): 从 -3 的位置 (1101) 在环上顺时针走一步。-3 -> -2。到达 -2 (1110)。
- 结果:-2 的表示就是 1110。这与代数计算 -2 = NOT(2) + 1 (即 1101 + 1 = 1110) 结果一致。
- 示例2: 求 -(-3) (4位系统)
- x = -3,二进制为 1101。
- 步骤1 (翻转所有位): NOT(-3) 是 0010。在2的补码中,0010 是 +2。
- 步骤2 (加1): 从 +2 的位置 (0010) 在环上顺时针走一步。+2 -> +3。到达 +3 (0011)。
- 结果:-(-3) 的表示就是 0011,即 +3。这与数学事实相符。
- 原文描述的歧义: 原文“顺时针少1刻度”的说法容易引起混淆。更精确的描述是:NOT(x) 的位置在 -x 的位置的“逆时针方向一步之遥”。或者反过来说,-x 的位置在 NOT(x) 的位置的“顺时针方向一步之遥”。
- 最负数的情况: 让我们看看最小负数 -4 (100)。
- x = -4 (100)。
- NOT(x) 是 011 (即 +3)。
- NOT(x) + 1 就是 011 + 1 = 100 (即 -4)。
- 几何上,从 +3 的位置顺时针走一步,越过了边界,到达了 -4。这个规则在边界情况下依然有效。
本段为2的补码取反操作(翻转位+1)提供了一个直观的几何心智模型。它将代数操作与在环形“风车”图上的移动联系起来:一个数的相反数 -x,可以通过先对其二进制按位取反,然后在环上将结果值顺时针移动一个位置来找到。
目的是为了超越纯粹的代数操作,给学习者一个“看得见、摸得着”的直观感觉。这种几何解释有助于建立更深刻的理解和记忆,让我们明白“翻转位”和“加1”这两个步骤并非随意组合,它们在模运算的环上有着明确的几何对应关系。
“2的补码取反 = 照镜子 + 往前挪一格”。
- “照镜子”(按位取反 NOT(x)):想象环的中心有一面特殊的“1的补码镜子”,一个数照镜子后会变成它的 NOT 值。
- “往前挪一格”(加1):镜子里的像(NOT(x))离真实的相反数 -x 总差那么一点点,所以镜中像需要再往前(顺时针)走一格,才能变成真正的相反数。
你站在一个圆形的房间里,墙上有8个门,分别标着-4到+3。你想去你当前位置 x 的“相反房间” -x。
你的导航仪告诉你:
- 首先,闭上眼睛,原地180度转身,面对你现在位置的“1的补码”房间 NOT(x)。
- 然后,向你右手边(顺时针)的隔壁房间走一步。
- 睁开眼,你就到达了 -x 房间。
这个两步操作法,就是“翻转位+1”的直观体现。
53.5. “翻转位+1”的正式证明
📜 [原文10]
- 从任何 $k$-位字 $X$(除了 $100 \ldots 000$)开始,并以 2 的补码表示它
- 设 $Y = X$ 并翻转所有位
- $X+Y=11 \ldots 1111$(使用二进制加法算法)
- 因此,$X+Y=-1$ 在 2 的补码表示中(在“风车”上从 $00 \ldots 0000$ 逆时针旋转 1 位)
- 然后 $X+Y+1=00 \ldots 0000$(使用二进制加法算法)
- 所以 $Y+1=-X$(并且回想 $Y$ 是 $X$ 翻转所有位)
这部分提供了“取反加一”操作为什么能得到相反数的代数证明。它非常简洁和巧妙。
- 前提设定:
- 我们有一个 k 位的二进制数 X。
- 这个证明对除了最小负数(100...0)之外的所有数都有效。(对于最小负数,我们之前已经分析过,它的取反会溢出)。
- 我们定义 Y 为 X 按位取反的结果。在C语言中,Y = ~X。
- 关键步骤1: X + Y:
- 一个数和它按位取反的结果相加,会发生什么?
- 例如,X = 0101。那么 Y = 1010。
- X + Y = 0101 + 1010 = 1111。
- 这个规律是普适的:对于任何 k 位的 X,X + ~X 的结果一定是 k 个1,即 11...11。因为在每一位上,不是 0+1 就是 1+0,结果都是 1,并且没有进位。
- 所以,$X+Y=11 \ldots 1111$。
- 关键步骤2: 解释 11...11:
- 在 k 位的2的补码表示法中,11...11 这个二进制模式代表什么值?
- 它代表 -1。
- 为什么?我们可以验证一下。对 -1 (11...11) 取反:
- 按位取反: 00...00
- 加1: 00...01 (即 +1)
- 既然 -(-1) 得到 +1,那么 11...11 的确就是 -1。
- 所以,我们从上一步得到 $X+Y=-1$。这里的 Y 也就是 ~X (X的按位取反)。所以我们有 $X + (\sim X) = -1$。
- 关键步骤3: 两边同时加1:
- 我们有等式 $X + Y = -1$。
- 在等式两边同时加上1: $(X + Y) + 1 = -1 + 1$。
- 右边 -1 + 1 = 0。
- 左边,根据加法结合律,可以写成 $X + (Y+1) = 0$。
- 结论:
- 从 $X + (Y+1) = 0$,我们可以推导出 $(Y+1) = -X$。
- 回想一下 Y 是什么?Y 是 X 按位取反的结果 (~X)。
- 所以,我们证明了 $(\sim X) + 1 = -X$。
- 这正是2的补码取反操作的定义:“翻转所有位,再加1,就得到相反数”。
- 示例1: 4位系统,X = 5
- X = 0101 (5)。
- Y = ~X = 1010 (这是2的补码的-6)。
- X + Y = 0101 + 1010 = 1111。
- 1111 在2的补码中是 -1。所以 X+Y = -1 成立。
- X + Y + 1 = 1111 + 0001 = (1)0000。结果是 0。
- 所以 X + (Y+1) = 0。
- 因此 Y+1 = -X。
- Y+1 = 1010 + 1 = 1011。
- 1011 是2的补码的 -5。
- -X 就是 -5。
- 结论 Y+1 = -X 得到验证。
- 示例2: 8位系统,X = -30
- +30 = 00011110。
- X = -30。先求-30的2的补码:00011110 -> 11100001 -> 11100010。所以 X = 11100010。
- Y = ~X = 00011101 (这是2的补码的29)。
- X + Y = 11100010 + 00011101 = 11111111。
- 11111111 是 -1。成立。
- (Y+1) = 00011101 + 1 = 00011110。这是 +30。
- -X = -(-30) = +30。
- 结论 Y+1 = -X 再次得到验证。
- 证明的前提: 这个证明排除了最小负数 100...0。让我们看看对它应用这个证明会发生什么。
- X = 1000 (假设4位,即-8)。
- Y = ~X = 0111 (即7)。
- X + Y = 1000 + 0111 = 1111 (即-1)。
- 到这里都没问题,$X+(\sim X) = -1$ 依然成立。
- X + Y + 1 = 0。
- Y + 1 = -X。
- Y+1 = 0111 + 1 = 1000 (即-8)。
- -X = -(-8) 应该是 +8。
- 所以我们得到 -8 = +8,这是一个矛盾。这个矛盾的根源在于 +8 无法在4位2的补码中表示,发生了溢出。所以代数推导本身没有错,是结果的解释(赋值)环节出了问题。
本段提供了一个严谨且优雅的代数证明,解释了为什么“按位取反再加一”这个操作能够得到一个数的相反数。证明的关键在于利用了 X + (~X) = -1 这个恒等式。
在给出了直观的几何解释之后,提供一个严格的数学证明是必要的。这满足了学习中从直观到严谨的认知过程。它告诉我们,2的补码的设计不仅仅是“碰巧好用”,其背后有坚实的数学原理支撑。
这个证明的核心可以看作是利用 -1 作为一个“中间人”或“桥梁”。
- 任何数 X 和它的“底片” ~X 加起来,总是能得到 -1 这个“通用参考点”。
- X + ~X = -1
- 这个关系就像 “你 和 你在镜子里的像,合起来总是构成一个稍微有点缺陷的整体(-1)”
- 为了得到一个完美的“0”(阴阳相消),我们还需要一点点“补偿”(+1)。
- X + (~X + 1) = 0
- 这就意味着 (~X + 1) 正好就是可以和 X “完美抵消”的那个东西,也就是 -X。
想象你在玩拼图。
- 一块拼图是 X。
- 它的“反色”拼图(颜色完全相反)是 ~X。
- 你发现,把 X 和 ~X 拼在一起,总是能拼成一个几乎完整的、但中心缺了一个小圆孔的黑色大圆盘。这个“缺了孔的圆盘”就是 -1。
- 为了得到一个完美的、没有任何瑕疵的“0”状态(比如一块纯白色的板子),你需要把 X 和 ~X 拼起来,然后再用一个“小圆片”(+1)把那个孔堵上。
- 所以,X + (~X + 1) = 0。
- 这说明,~X 加上那个“小圆片”1 所形成的组合体 (~X+1),就是 X 的完美“反物质”搭档 -X。
44. 表示 vs. 操作
14.1. k-位字 & 各种表示的范围
📜 [原文11]
- 给定一个 $k$-位字,可以表示的数字范围是:
- 无符号:0 到 $2^{k}-1$(例如,$k=8$,0 到 255)
- 有符号幅度:$-2^{k-1}+1$ 到 $2^{k-1}-1$(例如,$k=8$,-127 到 127 [2 种表示 0 的方式])
- 1 的补码:与有符号幅度相同(但负数表示方式不同)
- 2 的补码:$-2^{k-1}$ 到 $2^{k-1}-1$(例如,$k=8$,-128 到 127 [1 种表示 0 的方式])
这一部分是对之前所有内容的总结,系统地归纳了对于一个给定的字长k,四种不同表示法所能覆盖的数值范围。
- k-位字: 一个 k 位的二进制数,总共有 $2^k$ 种不同的模式(从全0到全1)。这 $2^k$ 个模式是我们能利用的全部“坑位”。
- 无符号 (Unsigned):
- 范围: 0 到 $2^k - 1$。
- 解释: 所有的 $2^k$ 个模式都用来表示非负数。最小的是 00...0 (0),最大的是 11...1。一个 k 位的全1二进制数,其值是 $2^{k-1} + 2^{k-2} + ... + 2^0 = 2^k - 1$。
- 示例 k=8: 范围是 0 到 $2^8 - 1 = 255$。共256个值。
- 有符号幅度 (Sign-Magnitude):
- 范围: $-(2^{k-1}-1)$ 到 $2^{k-1}-1$。
- 解释: 最高位是符号位,剩下 k-1 位是幅度位。
- 正数: 符号位为0。幅度位可以从 0...0 到 1...1 (k-1位)。最大的幅度是 $2^{k-1}-1$。所以正数范围是 1 到 $2^{k-1}-1$。再加上一个 +0。
- 负数: 符号位为1。幅度位同样最大是 $2^{k-1}-1$。所以负数范围是 -1 到 $-(2^{k-1}-1)$。再加上一个 -0。
- 总范围是 $[-(2^{k-1}-1), 2^{k-1}-1]$。
- 示例 k=8: k-1=7。范围是 $-(2^7-1)$ 到 $2^7-1$,即 -127 到 127。因为有+0和-0,总共能表示 $127 + 127 + 1 = 255$ 个唯一值,浪费了一个模式。
- 1的补码 (1's Complement):
- 范围: 与有符号幅度相同,$-(2^{k-1}-1)$ 到 $2^{k-1}-1$。
- 解释: 尽管负数的表示方法不同(通过按位取反),但它同样存在+0 (00...0) 和-0 (11...1) 的问题,所以它也浪费了一个位模式,导致其表示范围与有符号幅度完全一样。
- 示例 k=8: 范围是 -127 到 127。
- 2的补码 (2's Complement):
- 范围: $-2^{k-1}$ 到 $2^{k-1}-1$。
- 解释:
- 只有一个0的表示,所有 $2^k$ 个模式都被有效利用。
- 正数: 0...0 到 01...1。最高位为0。剩下 k-1 位能表示的最大值是 $2^{k-1}-1$。所以正数范围是 0 到 $2^{k-1}-1$。
- 负数: 最高位为1。它利用了符号与幅度中表示-0的那个模式 (10...0) 来表示最小的负数 $-2^{k-1}$。这使得负数比正数多一个。
- 示例 k=8: 范围是 $-2^7$ 到 $2^7-1$,即 -128 到 127。共256个值。
- 示例: k=4
- k=4, $2^k = 16$。
- 无符号: 0 到 $2^4-1 = 15$。
- 有符号幅度: $-(2^3-1)$ 到 $2^3-1$,即 -7 到 7。
- 1的补码: -7 到 7。
- 2的补码: $-2^3$ 到 $2^3-1$,即 -8 到 7。
- 范围的端点: 记忆这些范围公式时,特别注意 -1 和 +1 的位置。比如,无符号的最大值是 $2^k-1$ 而不是 $2^k$。2的补码的最小值是 $-2^{k-1}$ 而不是 $-2^{k-1}+1$。
- 对称性: 有符号幅度和1的补码的范围是关于0对称的。而2的补码的范围是不对称的,负数那边多一个。
- k 和 k-1: 在计算范围时,要分清指数是 k 还是 k-1。k决定了总模式数,k-1通常决定了有符号数幅度的大小。
本节内容是一个非常重要的总结性列表,它清晰地量化了四种整数表示法在给定字长 k 下的表示能力。通过比较它们的数值范围,我们可以再次看出2的补码在表示效率(没有浪费模式)和范围宽度(不对称但充分利用)上的优势。
目的是为了给程序员和系统设计者提供一个“速查手册”。在选择数据类型(如char, short, int, long)时,其背后对应的就是这些范围。理解这些范围的来源,对于避免溢出错误、进行正确的类型选择和数据转换至关重要。
想象你有 2^k 块积木,你要用它们来搭建一条数轴。
- 无符号: 你把所有积木都从0点开始向正方向铺,铺到了 $2^k-1$。
- 有符号幅度/1的补码: 你把积木分成两半。一半向正方向铺,一半向负方向铺。但你在0点那里不小心用了两块积木(一块叫+0,一块叫-0),导致数轴两端都短了一点。
- 2的补码: 你也把积木分成两半。但你很聪明,0点只用了一块积木。省下来的那块积木,你把它铺在了负半轴的最远端,让负半轴比正半轴长了一块积木的距离。
你有一个 k 位的二进制计数器。
- 无符号: 它就是一个简单的计数器,从0数到 $2^k-1$。
- 有符号幅度: 最高位的灯是红/绿灯(代表负/正),剩下k-1个灯是计数器。
- 1的补码: 一种奇怪的计数器,它的“全灭”和“全亮”状态都被当作0。
- 2的补码: 一个可以向前转也可以向后转的里程表。向前转是正数,向后转是负数。而且它被设计得刚刚好,转一整圈不多不少正好是 $2^k$ 个不同的读数。
55. 获取表示
15.1. 获取表示
📜 [原文12]
- 问:给定 8-位字长,10001011 的值是多少?
- 答:它是以无符号、有符号幅度、1 的补码还是 2 的补码表示?
- 无符号:$128+8+2+1=139$
- 有符号幅度:$-1 * (8+2+1)=-11$
- 1 的补码:01110100 的取反 $=-116$
- 2 的补码:01110101 的取反 $=-117$
- 注意:对于给定的一组位,当 \# 为负数时,2 的补码比 1 的补码小 1
这一部分通过一个具体的例子,生动地展示了“表示”和“值”之间的关系:同一串二进制位,在不同的解释规则(表示法)下,会对应完全不同的数值。
- 问题: 给定一个8位的二进制模式 10001011,问它的值是多少。
- 核心前提 (回答): 这个问题本身是“不完整”的。在回答之前,你必须先知道我们应该用哪一套“解码规则”。就像给你一串摩尔斯电码,你得先知道用的是英文还是法文的对应表。这里的“解码规则”就是无符号、有符号幅度、1的补码和2的补码这四种表示法。
- 分情况计算:
- 无符号 (Unsigned):
- 规则: 将每一位乘以其对应的权重($2^i$)并相加。
- 计算: 10001011 = $1 \cdot 2^7 + 0 \cdot 2^6 + 0 \cdot 2^5 + 0 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0$
- $= 128 + 0 + 0 + 0 + 8 + 0 + 2 + 1 = 139$。
- 有符号幅度 (Sign-Magnitude):
- 规则: 最高位是符号位(1代表负),其余7位是幅度。
- 计算:
- 符号: 最高位是 1,所以是负数。
- 幅度: 0001011 = $0 \cdot 64 + ... + 1 \cdot 8 + 0 \cdot 4 + 1 \cdot 2 + 1 \cdot 1 = 8+2+1 = 11$。
- 结果: -11。原文的 -1 * (8+2+1) 是一个简化的写法。
- 1的补码 (1's Complement):
- 规则: 因为最高位是 1,所以它是一个负数。要找出它的值,我们先将其按位取反,得到它对应的正数的绝对值。
- 计算:
- 按位取反: 10001011 -> 01110100。
- 计算这个正数的值: 01110100 = $0 \cdot 128 + 1 \cdot 64 + 1 \cdot 32 + 1 \cdot 16 + 0 \cdot 8 + 1 \cdot 4 + 0 \cdot 2 + 0 \cdot 1 = 64 + 32 + 16 + 4 = 116$。
- 因为原始数是负数,所以结果是 -116。
- 2的补码 (2's Complement):
- 规则: 因为最高位是 1,所以它是一个负数。要找出它的值,我们先减1再按位取反,或者用“取反加一”的逆操作。另一种更直接的方法是使用权重法。
- 计算 (方法一: 逆操作):
- 减1: 10001011 - 1 = 10001010。
- 按位取反: 10001010 -> 01110101。
- 计算这个正数的值: 01110101 = $64+32+16+4+1 = 117$。
- 所以结果是 -117。
- 计算 (方法二: 权重法):
- 最高位 1 的权重是 $-2^{8-1} = -128$。
- 其余位按正权重计算。
- 10001011 = $-128 + (0\cdot64 + ... + 1\cdot8 + 0\cdot4 + 1\cdot2 + 1\cdot1) = -128 + 11 = -117$。
- 原文的“01110101 的取反”描述得不准确,应该是“对10001011执行2的补码取反操作得到01110101”。
- 注意/观察:
- “对于给定的一组位,当 \# 为负数时,2 的补码比 1 的补码小 1”。
- 这个观察非常敏锐。在我们的例子中,同一个二进制模式 10001011,在1的补码下是-116,在2的补码下是-117。-117 确实比 -116 小1。
- 这是普适的规律。因为2的补码负数定义为 ~X + 1,而1的补码负数定义为 ~X(这里X是正数)。对于同一个正数X,它的两种负数表示之间就差了一个+1。这导致了对于同一个负数(比如-116),它的2的补码表示会和1的补码表示不同。反过来看,对于同一个二进制模式,如果它表示负数,那么它在2的补码下解读出的值,总是比在1的补码下解读出的值要“更负”一些(小1)。
- 示例: 4位字 1101
- 无符号: $8+4+1 = 13$。
- 有符号幅度: 符号为负,幅度为101 (5)。值为 -5。
- 1的补码: 负数。取反得0010 (2)。值为 -2。
- 2的补码: 负数。权重法: $-8 + 4 + 1 = -3$。
- 观察: 2的补码值(-3)比1的补码值(-2)小1。
- 计算方法的混淆: 学生在计算一个负的2的补码的值时,常常会错误地使用1的补码或有符号幅度的方法,或者忘记逆向操作的正确步骤(先减1再取反)。权重法通常更直接,不易出错。
- 正数的错觉: 对于最高位为0的二进制串,例如 01001011,这四种表示法的前三种(无符号,有符号幅度,1的补码,2的补码)给出的结果是完全相同的(都是75)。只有当最高位为1时,差异才会显现。
- 原文描述的简化: 原文中“...的取反”这种描述比较口语化,容易引起歧义。精确的说法应该是“对...进行1的补码取反操作”或“...是...的1的补码表示”。
本节通过一个具体的8位二进制数,清晰地演示了“上下文(解释规则)决定意义”这一核心思想。同一串0和1,在四种不同的表示法下,代表了四个完全不同的数字。这也再次突显了在进行任何二进制层面的讨论或编程时,明确其数据类型(即解释规则)是多么重要。
本节的目的是进行一次“横向对比”的实践。它强迫学习者主动运用前面学到的四种表示法的解码规则,从而加深理解和记忆。同时,它也作为一个警示,提醒我们不能孤立地看待一串二进制码,必须将其放在特定的“表示法”背景下才能解读其真正的数值。
这就像看一幅“双关图”(比如著名的“是兔子还是鸭子?”)。
- 二进制模式 10001011: 就是那幅模棱两可的图画。
- 四种表示法: 就是四种不同的“观看角度”或“心理预设”。
- 当你被告知“这是一只鸭子”(使用无符号法),你就看到了139。
- 当你被告知“这是一只兔子”(使用2的补码法),你就看到了-117。
- 图画本身没有变,变的是你的解读框架。没有上下文,图画的意义是不确定的。
想象你收到一条加密信息“10001011”。
- 你的密码本上有四种不同的解密方案。
- 方案A (无符号): 告诉你这是一个藏宝图,地点在139号大街。
- 方案B (有符号幅度): 告诉你这是一个银行账户,欠了11元钱。
- 方案C (1的补码): 告诉你这是一个飞行高度,在海平面下116米。
- 方案D (2的补码): 告诉你这是一个温度读数,零下117度。
- 在发送者告诉你应该用哪种方案之前,这条信息是毫无用处的,甚至是危险的。
66. 表示 vs. 操作 (总结)
📜 [原文13]
- 我们已经讨论了表示整数的各种方法
- 无符号、有符号幅度、1 的补码、2 的补码
- 还有以位为单位的操作,名称相同
- 1 的补码操作:翻转所有位
- 2 的补码操作:翻转所有位并(BAA)加 1
- 操作可以在数字上执行,无论表示形式如何
- 例如,设 10111 是一个有符号幅度形式的数字(值为 -7)
- 在 10111 上执行 2 的补码(操作) $=01001$(在有符号幅度形式中值为 9)
- 观察:
- 当数字使用 2 的补码表示时,2 的补码操作会取反该数字
- 当数字使用 1 的补码表示时,1 的补码操作会取反该数字
这一部分做了一个非常重要且精妙的区分:表示法(Representation)和操作(Operation)。这两者名字可能相同(如“2的补码”),但概念上是完全独立的。
- 表示法 (Representation):
- 这是指一套“解码规则”,用于将一个二进制模式映射到一个数学值。
- 我们已经学了四种表示法:无符号、有符号幅度、1的补码表示、2的补码表示。
- 它回答的问题是:“这串0和1是什么数字?”
- 操作 (Operation):
- 这是指一个在二进制位上执行的“算法”或“过程”。它不关心这些位的含义是什么,只管对它们进行变换。
- 1的补码操作: 定义为“按位取反”(NOT)。
- 2的补码操作: 定义为“按位取反,再加1”(NOT(x) + 1)。
- 它回答的问题是:“对这串0和1做什么?”
- 核心思想:操作与表示的分离:
- “操作可以在数字上执行,无论表示形式如何”。
- 这意味着,我可以拿一个用A表示法代表的数,然后对它的二进制位执行B操作。这是一个完全合法的行为,尽管结果可能不直观。
- 示例分析:
- 初始状态:
- 数字是 10111。
- 它的表示法是“有符号幅度”。
- 根据有符号幅度规则,最高位1是负号,0111是7。所以它的值是 -7。
- 执行操作:
- 我们要执行的操作是“2的补码操作”,即“按位取反,再加1”。
- 1. 按位取反: 10111 -> 01000。
- 2. 加1: 01000 + 1 = 01001。
- 结果解读:
- 操作的结果是一个新的二进制模式 01001。
- 我们仍然使用原来的表示法——“有符号幅度”——来解读这个结果。
- 根据有符号幅度规则,最高位0是正号,1001是9。所以 01001 的值是 +9。
- 整个过程: 我们对一个值为-7的数(它恰好是用有符号幅度表示的),执行了一个名为“2的补码”的位操作,得到了一个值为+9的数。这个过程本身是纯粹的位游戏,-7和+9之间没有明显的数学关系。
- 最后的观察(关键联系):
- “当数字使用 2 的补码表示时,2 的补码操作会取反该数字”。
- 这解释了为什么“2的补码操作”这么有用。当“表示法”和“操作”匹配时,这个操作就获得了明确的数学意义——取反(negation)。
- 例如:数是 0011 (+3),表示法是2的补码。对其执行“2的补码操作”(NOT+1),得到 1101。在2的补码表示法中,1101的值是-3。看,+3 变成了 -3。
- “当数字使用 1 的补码表示时,1 的补码操作会取反该数字”。
- 同理,当表示法和操作匹配时,操作获得了取反的意义。
- 例如:数是 0011 (+3),表示法是1的补码。对其执行“1的补码操作”(NOT),得到 1100。在1的补码表示法中,1100的值是-3。
- 示例: 不匹配的操作和表示
- 初始状态:
- 数字 1110。
- 表示法: 2的补码 (5位系统,假设是11110)。值为 -2。
- 执行操作:
- 1的补码操作 (按位取反)。
- 11110 -> 00001。
- 结果解读:
- 我们仍然用2的补码表示法来解读 00001。
- 值为 +1。
- 总结: 我们对一个值为-2的数(用2的补码表示),执行了1的补码操作,得到了一个值为+1的数。
- 术语混淆: 这是最大的易错点。当别人说“2的补码”时,一定要搞清楚他指的是一种表示法,还是一个位操作。上下文通常会很清楚,但初学者容易混淆。
- 误认为操作总是有意义的: 对一个无符号数执行“2的补码操作”是完全合法的位运算,但其结果的算术意义就不再是“取反”了。例如,对无符号数5 (0101) 执行2的补码操作,得到 1011 (无符号值11)。5和11之间没有简单的“取反”关系。
本节清晰地区分了“表示法”(解码规则)和“位操作”(变换算法)这两个概念。虽然它们可能同名,但本质不同。一个操作的数学意义(如“取反”)只有在它被应用于与之匹配的表示法表示的数字上时才会显现。这个区分是理解底层计算原理的关键一步。
目的是为了澄清一个非常容易混淆的术语,并建立一个更精确的思维框架。它让我们认识到,计算机底层的世界是纯粹的位操作,而这些操作的“意义”是我们(通过编译器和语言设计)赋予的。只有当操作和表示法“同频”时,我们才能得到期望的算术结果。
- 表示法: 就像一本“字典”(比如英汉字典,法汉字典)。它告诉你一个“词”(二进制模式)的“意思”(数值)。
- 操作: 就像一个“文字游戏规则”(比如“把每个字母替换成字母表里的下一个字母”)。
- 你可以拿一个英文单词(用“英语表示法”的词),然后对它玩“法语的文字游戏”。这是可以做到的,但结果可能是一个毫无意义的字母组合。
- 只有当你拿一个英文单词,玩“英语的文字游戏”(比如“倒序拼写”),结果才有意义(变成一个倒着写的英文词)。
- 这里的关键是,2的补码操作 只有在作用于 2的补码表示 的数字上时,其意义才是“取反”。
想象你有一把钥匙 10111。
- 表示法: 这把钥匙能开哪扇门?你说它能开“有符号幅度”这扇门,门上写着-7。
- 操作: 现在你有一个“钥匙改装工具”,名叫“2的补码改装器”。它会把任何钥匙都“锉一下再加个齿”。
- 你把 10111 这把钥匙用这个工具改装了一下,变成了一把新钥匙 01001。
- 这把新钥匙能开哪扇门?你还是用“有符号幅度”的锁去试,发现它打开了写着 +9 的门。
- 你发现,如果一把钥匙是用来开“2的补码”门的,那么用“2的补码改装器”改完后,正好能打开它相反数的那扇门。这个工具和这种门是“配套”的。
77. 自动化减法
17.1. 自动化减法示例
📜 [原文14]
- 问:为什么我们对 2 的补码感兴趣,尽管它看起来如此不直观?
- 答:自动化减法(即加符号相反的 \#)要容易得多
- 例如,字长 6,使用有符号幅度表示执行 14-21
- 有符号幅度有很多潜在的“繁重工作”
- 例如,翻转顶部 & 底部,“从较高位借位”等。
这部分通过一个反例——使用有符号幅度进行减法——来突出2的补码的优越性。
- 核心问题: 为什么我们要忍受2的补码这种看起来不那么直接的表示法?
- 核心答案: 因为它能让计算机硬件极大地简化减法运算。计算机的ALU(算术逻辑单元)天生就有一个高效的加法器。如果能把减法也变成加法,那么就不需要再额外设计一个复杂的减法器了。2的补码正好能实现这个目标:A - B 可以通过 A + (-B) 来计算,而 -B 的2的补码可以通过简单的“取反+1”位操作得到。
- 有符号幅度的“繁重工作”: 为了说明这一点,原文展示了用有符号幅度表示法计算 14 - 21 的复杂过程。
- 初始状态:
- +14 在6位有符号幅度下是 001110 (符号0,幅度14)。
- +21 在6位有符号幅度下是 010101 (符号0,幅度21)。
- 减法过程:
- 14 - 21 是一个小数减大数,结果应该是负数。
- 人类做这个减法时,会下意识地把它转换成 -(21 - 14)。
- 计算机硬件要模仿这个过程,就需要一系列的判断和操作:
- 比较幅度: 硬件需要先比较 14 (001110) 和 21 (010101) 的大小。它发现 21 > 14。
- 翻转操作数: 因为是被减数的幅度小,所以硬件需要交换两个数的幅度,变成用大幅度减小幅度,即 21 - 14。
- 确定结果符号: 因为是小数减大数,结果的符号应该是负号。硬件需要记下这个最终符号。
- 执行减法: 现在硬件对两个幅度 010101 和 001110 执行二进制减法。这涉及到复杂的“借位”逻辑,和我们做十进制减法一样。
```
010101 (21)
- 001110 (14)
----------
000111 (7)
```
- 组合结果: 最后,硬件将第3步确定的负号(1)和第4步得到的幅度 000111 组合起来,得到最终结果 100111,它在有符号幅度下表示 -7。
- 总结: 整个过程涉及到:比较大小、可能地交换操作数、确定符号、执行带借位的减法、最后再组合。这一系列“如果...那么...”的逻辑,对于硬件设计来说是非常复杂和低效的。
- 示例: 用有符号幅度计算 -14 - 21
- -14 是 101110,+21 是 010101。
- 这是一个负数减正数,等于负数加负数: (-14) + (-21)。
- 硬件需要:
- 判断两个数符号。发现一个是负,一个是正,且是减法。或者发现是两个负数相加。
- 取出两个数的幅度: 14 和 21。
- 将两个幅度相加: 001110 + 010101 = 100011 (35)。
- 确定结果符号: 负数加负数,结果是负数。
- 组合结果: 符号1 和 幅度100011 -> 1100011。在6位系统里,这是溢出了,因为35超出了6位幅度能表示的范围(最大31)。
- 减法和加法的不同逻辑: 在有符号幅度中,加法和减法是完全不同的过程。A+B 和 A-B 都需要根据A和B的符号分成四种情况(正+正,正+负,负+正,负+负)来处理,非常繁琐。
- 硬件实现: 这种复杂的逻辑判断意味着需要更多的门电路、更长的计算延迟和更大的功耗。
本节通过展示有符号幅度减法的复杂性——需要比较大小、交换数字、处理借位、单独判断符号——来反衬出“将减法转换为加法”这一思路的巨大价值。它雄辩地证明了,2的补码之所以被采纳,正是因为它能用一套统一、简单的加法硬件来“自动化”所有加减运算。
目的是为了让学习者深刻体会到“优雅的”硬件设计是什么样的。通过展示一个“笨拙”的设计(有符号幅度的减法器),来 appreciation 2的补码所带来的“简洁之美”。这是一种通过对比来加强理解的教学方法。
- 有符号幅度减法: 就像一个做事死板的机器人。你让它算 14-21,它不会直接算。它会先拿出两个尺子量一下14和21谁长,发现21长。然后它把题目改成 21-14,算出来是7,然后自言自语:“哦,原来是小数减大数,那我得在答案前面加个负号”。整个过程充满了判断和特殊处理。
- 2的补码减法: 像一个聪明的机器人。你让它算 14-21,它二话不说,直接把 21 扔进一个“反转机”里变成了 -21 的代码,然后把 14 和这个新代码扔进一个“加法机”里。出来的结果直接就是 -7 的代码。一步到位,没有如果。
想象你在厨房做菜。
- 有符号幅度减法: 菜谱上写着“减去21克盐”。你需要:1. 称一下盘子里现在有多少盐(14克)。2. 比较一下,发现不够减。3. 于是你把菜谱反过来想:“相当于净增加 -7克盐”。4. 但你没有负的盐,所以你先把所有盐(14克)都取出来,再重新称21克盐,再从这21克里称出14克放回盘子里,剩下的7克扔掉,最后在盘子旁边贴个条“这是一个欠了7克盐的菜”。过程极其复杂。
- 2的补码减法: 菜谱上写着“减去21克盐”。你有一个“反物质盐瓶”(2的补码的负数)。你直接从这个瓶子里取出“21克反物质盐”加到盘子里。盘子里的14克盐和“21克反物质盐”一中和,自动就变成了“-7克盐”的状态。简单快捷。
88. 2 的补码减法:利用 BAA
18.1. 补码减法示例
📜 [原文15]
- 只需取反减数(减法中的底数)并加
- 例如,字长 6,使用 2 的补码表示执行 14-21
2 的补码减法:利用 BAA
- 只需取反减数(减法中的底数)并加
- 例如,字长 6,使用 2 的补码表示执行 14-21

$X=111001, -X=000111=7, X=-7$
这一部分紧接上一节,正面演示了使用2的补码执行减法是多么简洁高效。
- 核心方法: “只需取反减数(减法中的底数)并加”。
- 这句话是2的补码减法的操作口诀。
- “减数” (Subtrahend): 在 A - B 中,B 是减数。
- “取反”: 这里的“取反”指的是数学上的取反(negation),即求相反数。在2的补码系统中,这个操作对应于“按位取反再加1”的位操作。
- 所以,计算 A - B 的完整流程是:
- 保持 A 的二进制不变。
- 计算 B 的2的补码相反数,即 ~B + 1。
- 将 A 和 ~B + 1 用标准的二进制加法算法(BAA)相加。
- 示例演示: 14 - 21,使用6位2的补码。
- 字长 k=6。范围是 $[-2^{5}, 2^{5}-1]$,即 [-32, 31]。
- +14 的6位2的补码是 001110。
- +21 的6位2的补码是 010101。
- 步骤1: 取反减数
- 减数是 21 (010101)。我们需要计算 -21 的2的补码。
- 按位取反: 010101 -> 101010。
- 加1: 101010 + 1 = 101011。
- 所以,-21 的2的补码是 101011。
- 步骤2: 相加
- 现在问题变成了 14 + (-21)。
- 二进制计算: 001110 + 101011
```
11111 (进位)
001110 (14)
+ 101011 (-21)
----------
111001 (-7)
```
- 结果解读:
- 计算结果是 111001。
- 这是一个负数。我们来验证它的值。
- 逆操作:减1 -> 111000 -> 按位取反 000111。
- 000111 是 7。所以 111001 是 -7。
- 数学结果 14 - 21 = -7。
- 计算机的计算结果与数学结果完全一致。没有判断,没有借位,只有一次“取反+1”和一次加法。
- 图片和公式的解释:
- 图片清晰地展示了上述的计算过程。
- 最后的 $X=111001, -X=000111=7, X=-7$ 是对结果的验证。它表明,如果你对结果 111001 (X) 执行2的补码取反操作,你会得到 000111,它的值是 7,这说明原来的 X 确实是 -7。
- 示例1: 8位系统, 100 - 50
- A = 100 (01100100)
- B = 50 (00110010)
- 计算 -B (即 -50):
- ~B: 11001101
- ~B+1: 11001110
- 加法 A + (-B):
```
01100100 (100)
+ 11001110 (-50)
-----------
(1)00110010 (50)
```
- 结果 00110010,就是 50。正确。
- 示例2: 8位系统, -100 - 30 (导致溢出)
- A = -100。+100是01100100 -> ~是10011011 -> +1是10011100。
- B = 30 (00011110)。
- 计算 -B (即 -30):
- ~B: 11100001
- ~B+1: 11100010
- 加法 A + (-B):
```
1 1 (进位)
10011100 (-100)
+ 11100010 (-30)
-----------
(1)01111110 (126)
```
- MathResult = -130。这超出了8位2的补码范围 [-128, 127]。
- CompuResult = 01111110,即 +126。
- 发生了溢出。两个负数相加得到了一个正数。
- 验证模运算: $126 \equiv -130 \pmod{256}$ (因为 $126 = -130 + 256$)。
- 对谁取反: 一定要搞清楚是减数(第二个数字)需要被取反,而不是被减数。
- 取反操作的精确含义: “取反”在2的补码语境下,特指“按位取反再加一”,而不是简单的按位取反。
- 减法溢出: 减法同样会发生溢出。A - B 发生溢出的条件,等价于 A + (-B) 发生溢出的条件。例如,一个正数减一个负数,如果结果太大就会正向溢出。一个负数减一个正数,如果结果太小就会负向溢出。
本节通过一个清晰的、按部就班的例子,展示了2的补码减法的“魔法”:它将一个复杂的减法问题,通过一次简单的位操作(求补),转化成了一个纯粹的加法问题,然后利用高效的二进制加法算法(BAA)一举解决。这正是2的补码成为现代计算机基石的核心原因。
在上一节“批判”了有符号幅度之后,本节的目的是“立”,即正面展示2的补码方案是多么的优秀和简洁。通过这种“一反一正”的对比,让学习者对2的补-码的必要性和优越性建立起牢固的认识。
回到“聪明的机器人”模型。这个机器人只有一个工具:“加法锤”。
- 当被要求计算 A - B 时,机器人不换工具。
- 它先把 B 扔进一个“反转黑洞”里,出来一个 B' (即 -B 的2的补码)。
- 然后它拿起“加法锤”,把 A 和 B' 敲在一起。
- 最终得到的产物就是正确答案。
- 整个流程高度统一、自动化,不需要思考和判断。
你是一个银行出纳,你的任务是计算 账户A - 账户B。
- 你不需要做减法。你的流程是:
- 找到账户B的账本。
- 拿出一张特殊的“复印纸”(2的补码取反操作),盖在账本上复印一下,得到一张“负债单” -B。
- 把你手里的账户A的存款单和这张“负债单” -B 一起用加法计算器加起来。
- 计算器显示的结果就是最终的净值。整个银行系统只需要加法计算器,而不需要减法计算器。
99. 检测溢出
📜 [原文16]
- 问:如何判断计算结果是否溢出(即结果无法在字长约束内表示)
- 例如,4-位字,无符号:1110 + $1010 (14 + 10)$
- 结果是 24,无法在 4-位无符号中表示(只有 0-15 的值)
- 因此,溢出
- 无符号检测容易:
- 加法溢出
对于无符号 | 111 |
| :--- |
|---|
| $\underline{1010}$ |
| 1000 |
- 减法:减数大于 \#(结果为负),则溢出
这部分开始讨论一个至关重要的问题:既然运算可能溢出,那么计算机硬件如何知道溢出发生了呢?本节首先讨论最简单的情况:无符号整数的溢出检测。
- 溢出的定义: 溢出(Overflow)的根本定义是“计算结果无法在给定的字长和表示法下正确表示”。
- 无符号数溢出:
- 加法溢出:
- 对于 k 位的无符号数,其表示范围是 [0, 2^k - 1]。
- 当两个无符号数相加,其数学和大于等于 $2^k$ 时,就发生了溢出。
- 检测方法: 在执行 k 位的二进制加法时,如果最高位(第 k-1 位)向外产生了进位(carry-out),则发生了溢出。
- 示例分析:
- 计算 14 + 10 在4位无符号系统中。
- 14 是 1110,10 是 1010。
- 数学结果是 24。4位无符号范围是 [0, 15]。24 超出范围,溢出。
- 二进制加法:
- 我们看到,从最高位(左数第一位)的 1+1 产生了一个进位 1,这个进位跑到了第5位的位置上。这个“跑出来的进位”就是溢出的标志。CPU中的状态寄存器会有一个“进位标志位”(Carry Flag),它会捕获这个最高位的进位。如果Carry Flag被置为1,就表示发生了无符号加法溢出。
- 计算机保留的4位结果是 1000 (8),这与 24 mod 16 = 8 相符。
- 减法溢出:
- 对于无符号数,它们不能表示负数。所以任何导致结果为负的减法,都是溢出。
- 检测方法: A - B,如果 B > A,则发生溢出。在硬件层面,这通常也是通过检查进位/借位标志位来判断的。在执行 A - B (即 A + ~B + 1) 时,如果没有从最高位产生进位,则说明发生了“借位”,即无符号减法溢出。
- 示例: 10 - 14 在4位无符号系统中。
- 10 是 1010。
- -14 的2的补码是: 14 (1110) -> ~ (0001) -> +1 (0010)。
- 1010 + 0010 = 1100 (12)。
- 从最高位没有产生进位。这标志着溢出。
- 结果 12 与 -4 mod 16 = 12 相符。
- 示例1: 8位无符号加法溢出
- 计算 200 + 100。
- MathResult = 300。8位无符号范围是 [0, 255]。溢出。
- 200 = 11001000。
- 100 = 01100100。
- 11001000 + 01100100 = (1)00101100。
- 产生了最高位进位 1,所以CPU的Carry Flag置位,标志溢出。
- CompuResult = 00101100 (44)。
- 验证: 44 = 300 - 256。
- 示例2: 8位无符号减法溢出
- 计算 100 - 200。
- MathResult = -100。无符号数不能为负,溢出。
- 100 = 01100100。
- -200 的2的补码: 200(11001000) -> ~(00110111) -> +1(00111000)。
- 01100100 + 00111000 = 10011100 (156)。
- 最高位没有产生进位(Carry Flag为0)。标志着无符号减法溢出。
- 验证: 156 = -100 + 256。
- 把Carry Flag和Overflow Flag搞混: 很多CPU有两个不同的状态标志位。Carry Flag (CF) 主要用于无符号运算的溢出检测。而Overflow Flag (OF) 用于2的补码(有符号)运算的溢出检测。它们判断的逻辑是不同的。本节只讨论了CF。
- 减法溢出检测的复杂性: 用“没有进位”来判断无符号减法溢出虽然是硬件的实现方式,但从人的角度理解 B > A 更直观。
本节介绍了无符号整数算术的溢出检测方法,这个方法相对简单:对于加法,检查最高位是否产生进位;对于减法,检查是否需要“借位”(即被减数 < 减数)。CPU通过硬件中的进位标志位(Carry Flag)来自动完成这个检测。
目的是在深入讨论更复杂的2的补码 溢出检测之前,先从一个简单、直观的例子入手。这有助于建立溢出检测的基本概念,并为后续的对比和深入学习打下基础。
- 无符号加法溢出: 就像往一个杯子里倒水。杯子的容量是 2^k-1。如果你倒的水(两个数之和)超过了杯子的容量,水就会从杯口溢出来。那个“溢出来的水”就是最高位的进位(Carry)。
- 无符号减法溢出: 就像你账户里只有100块钱(无符号数不能透支),但你想买一个200块的东西。你的钱不够,这就是溢出。
想象一个只能显示0到99的两位数计数器。
- 加法溢出: 计数器显示98。你让它加5。它会这样变化: 98 -> 99 -> 00 -> 01 -> 02 -> 03。最终显示03。同时,计数器旁边的一个小红灯(Carry Flag)亮了,告诉你“刚刚滚了一圈!”。
- 减法溢出: 计数器显示02。你让它减5。它会这样变化: 02 -> 01 -> 00 -> 99 -> 98 -> 97。最终显示97。同时,另一个小蓝灯(Borrow Flag,本质上是Carry Flag的反状态)亮了,告诉你“刚刚反向滚了一圈!”。
1010. 2 的补码中的溢出检测很简单
📜 [原文17]
| -如果最终两个进位匹配,则没有溢出 - 如果不同,则溢出 - 例如,字长 $=4$ |
|||
|---|---|---|---|
| $5+1=6$ | $-5+-3=-8$ | $-2+7=5$ | $-2+-7=-9$ |
| 00 | 11 | 11 | 10 |
| + | + | + | + |
| $\underline{0001}$ | $\underline{1101}$ | 0111 | $\underline{1001}$ |
| 0110 | 1000 | 0101 | 0111 |
- 需要考虑 3 种情况:
- 两个 \# 都是正数(即最高位都是 0)
- 两个 \# 都是负数(即最高位都是 1)
- 一个是正数(最高位 0),另一个是负数(最高位 1)
这部分介绍了2的补码(有符号数)加法中一种非常巧妙且高效的溢出检测方法。
- 核心规则: “如果最终两个进位匹配,则没有溢出。如果不同,则溢出。”
- “最终两个进位”指的是什么?它们是:
- 进位到最高有效位(MSB)的进位。我们称之为 C_in_msb。
- 从最高有效位(MSB)产生的进位。我们称之为 C_out_msb。
- 所以,溢出的条件是 C_in_msb != C_out_msb。在逻辑电路中,这可以用一个异或门(XOR)来简单实现:Overflow = C_in_msb XOR C_out_msb。
- 这个规则的美妙之处在于它完全不依赖于操作数的符号,是一个纯粹的、基于进位的硬件级别判断。
- 表格示例分析 (字长k=4):
- Case 1: 5 + 1 = 6
- 5=0101, 1=0001。
- 0101 + 0001。
- 进位到MSB(第3位)的进位是0。(C_in_msb=0)
- 从MSB产生的进位是0。(C_out_msb=0)
- C_in_msb == C_out_msb (0 == 0)。没有溢出。结果 0110 (6) 正确。
- 原文表格中的00可能是指这两个进位。
- Case 2: -5 + (-3) = -8
- -5=1011, -3=1101。
- 1011 + 1101。
- 进位到MSB的进位是1。(来自0+1和前一位的进位1)
- 从MSB产生的进位是1。(1(cin)+1+1=11)
- C_in_msb == C_out_msb (1 == 1)。没有溢出。结果 1000 (-8) 正确。
- 原文表格中的11指这两个进位。
- Case 3: -2 + 7 = 5
- -2=1110, 7=0111。
- 1110 + 0111。
- 进位到MSB的进位是1。(来自1+1和前一位的进位1)
- 从MSB产生的进位是1。(1(cin)+1+0=10)
- C_in_msb == C_out_msb (1 == 1)。没有溢出。结果 0101 (5) 正确。
- 原文表格中的11指这两个进位。
- Case 4: -2 + (-7) = -9 (溢出)
- -2=1110, -7=1001。
- 1110 + 1001。
- 进位到MSB的进位是0。(1+0和前一位进位1,1+1+0=10,所以进位是1...啊我算错了,1+0+1=10,进到MSB是1)
- 让我重新计算 -2+(-7):
```
11 (内部进位)
1110 (-2)
+ 1001 (-7)
-------
(1)0111 (7)
```
- 进位到MSB的进位是 1 (来自 1+0 和更前一位的进位 1)。C_in_msb = 1。
- 从MSB产生的进位是 1 (来自 1(cin) + 1 + 1 = 11)。C_out_msb = 1。
- 所以 1 == 1,应该没有溢出... 但 -2+(-7) 结果是 -9,明明溢出了。
- 让我重新审视原文表格的 10。10 意味着 C_out_msb=1, C_in_msb=0。
- 这说明我对进位的计算有误。再来一次 -2+(-7):
- 1110 + 1001
- 最低位: 0+1=1
- 第二位: 1+0=1
- 第三位: 1+0=1 (这里 C_in_msb = 0)
- 最高位: 1+1=10 (这里 C_out_msb = 1)
- 啊哈!C_in_msb = 0, C_out_msb = 1。0 != 1。溢出!
- 结果是 0111 (+7)。错误。
- 公式示例分析: 7+7=14
- 7=0111。
- 0111 + 0111。
- 进位到MSB的进位是 1 (来自1+1和前一位的进位1)。C_in_msb = 1。
- 从MSB产生的进位是 0 (来自1(cin)+0+0=1)。C_out_msb = 0。
- C_in_msb != C_out_msb (1 != 0)。溢出!
- 结果 1110 (-2)。错误。
- 原文公式下面画的 0 和 1 (我猜 0111上方的0和1?) 可能就是指 C_out 和 C_in。C_out=0, C_in=1。
- 按符号情况分析:
- 这个溢出检测规则也可以从操作数的符号来理解,这引出了另一种等价的判断方法。
- 正数 + 正数: 结果必须是正数。如果结果变成了负数(即结果的MSB为1),则溢出。
- 负数 + 负数: 结果必须是负数。如果结果变成了正数(即结果的MSB为0),则溢出。
- 正数 + 负数: 结果的绝对值不会超过两个数中绝对值较大的那个,所以永远不会溢出。
- 示例1: 6 + 3 (4位)
- 6=0110, 3=0011。
- 0110 + 0011 = 1001 (-7)。
- C_in_msb=1, C_out_msb=0。1 != 0 -> 溢出。
- 用符号判断:正+正,结果为负。溢出。
- 示例2: -6 + (-4) (4位)
- -6=1010, -4=1100。
- 1010 + 1100 = (1)0110 (+6)。
- C_in_msb=0, C_out_msb=1。0 != 1 -> 溢出。
- 用符号判断:负+负,结果为正。溢出。
- 手动计算进位: 手动计算 C_in_msb 和 C_out_msb 容易出错,需要非常仔细。
- 两种判断方法等价: “进位不匹配”规则和“符号不符合预期”规则是完全等价的,它们是同一现象的两种不同描述。硬件层面用前者,人类思考用后者更直观。
- 只适用于加法: 这个检测规则是针对加法(包括A+(-B)形式的减法)设计的。
本节介绍了判断2的补码加法是否溢出的两种等价方法:
- 硬件方法: 检查进入最高位的进位和从最高位出去的进位是否不同。不同则溢出。
- 逻辑方法: 检查操作数和结果的符号。同号相加,结果异号,则溢出。异号相加,永不溢出。
这两种方法都非常高效,使得溢出检测在CPU中可以快速完成。
目的是解决之前留下的一个关键问题:如何知道2的补码运算出错了?提供了可靠、高效的溢出检测方法,是构建一个完整的、健壮的算术逻辑单元(ALU)的最后一块拼图。
“进位不匹配”的直觉模型:
- C_in_msb: 代表了低位加法的结果是否“大到”需要向符号位“求助”(进位)。
- C_out_msb: 代表了加上符号位本身后,整个数是否“大到”要“冲出”k位的范围。
- 溢出就发生在这两种“大”的判断不一致时。
- 正+正溢出 (C_in=1, C_out=0): 低位部分已经很大了,需要向符号位进位(C_in=1)。但因为两个符号位都是0,加上进位1后,符号位变成了1,没有产生向外的进位(C_out=0)。结果的符号从正变成了负。
- 负+负溢出 (C_in=0, C_out=1): 低位部分不大,没向符号位进位(C_in=0)。但两个符号位都是1,1+1=10,结果的符号位变成了0,还向外产生了进位(C_out=1)。结果的符号从负变成了正。
想象符号位是一个特殊的“经理”位,其他位是“员工”位。
- C_in_msb: 是员工们的工作量是否大到需要向经理汇报(进位)。
- C_out_msb: 是经理处理完自己的工作和员工的汇报后,是否导致整个项目“爆掉”(向更高层进位)。
- 溢出就像:
- 员工们忙得要死,向经理求助 (C_in=1)。但经理(和另一个正数经理)自己很闲,他处理完汇报后说“项目没问题” (C_out=0)。结果整个团队(结果数)的状态从“正常”(正)变成了“危机”(负)。
- 员工们自己搞定了,没向经理汇报 (C_in=0)。但经理(和另一个负数经理)自己就在处理一个烂摊子,他们俩一合计,直接让项目“爆了” (C_out=1)。结果整个团队的状态从“危机”(负)变成了“看起来一切正常”(正)。
- 只有当经理的判断 (C_out) 和员工的状况 (C_in) 一致时,项目状态才是可信的。
1111. 为什么 2 的补码溢出检测有效的证明
111.1. 情况1:两者皆正
📜 [原文18]
- 情况 1:两者皆正:
- 写下两个最高位进位为 A 和 B
- 写下两个最高位进位为 $A$ 和 $B \quad A B$
- $A=$ 进位 B $+0+0 O X_{k-2} X_{k-3} \ldots X_{0}$
$O Y_{k-2} Y_{k-3} \ldots Y_{0}$
- A 始终为 0!
- 最高位 $= B+0+0$
- $B=1$:将结果解释为负数?
错误
- $B=0$:正常(刚刚执行了无符号 $K-1$ 位
加法)
这部分开始对上一节提出的溢出检测规则进行分情况证明。首先证明第一种情况:两个正数相加。
- 设定:
- 我们有两个 k 位的2的补码正数 X 和 Y。
- 因为是正数,它们的最高位(MSB,第k-1位)都是 0。
- X = 0 X_{k-2} ... X_0
- Y = 0 Y_{k-2} ... Y_0
- A 在这里代表 C_out_msb (从最高位产生的进位)。
- B 在这里代表 C_in_msb (进位到最高位的进位)。
- 分析 A (C_out_msb):
- 最高位的加法是 A = B + 0 + 0。这里的两个 0 是 X 和 Y 的符号位。
- B 是从第 k-2 位传来的进位,它要么是 0 要么是 1。
- 所以 A = B。C_out_msb = C_in_msb。
- 等等,原文的推导似乎有点问题或表达不清。
- 让我们严格按照加法来:最高位的计算是 (结果的MSB, A) = B + 0 + 0,这里 (a,b) 表示和为b,进位为a。
- B+0+0 的和就是 B,进位是 0。
- 所以,结果的MSB就是 B,而 A (从最高位出去的进位) 始终为0!
- C_out_msb (即A) = 0。
- 分析 B (C_in_msb):
- B 是从低 k-1 位(数值部分)加法产生的进位。
- B 完全取决于 X_{k-2}...X_0 和 Y_{k-2}...Y_0 的和。
- 结合分析,判断溢出:
- 我们已经确定 A = C_out_msb = 0。
- 溢出规则是 A != B。
- 所以,当两个正数相加时,溢出发生的条件是 0 != B,即 B = 1。
- 不溢出的条件是 A == B,即 B = 0。
- 解读两种情况:
- 情况一: B = 0 (不溢出)
- 从数值部分没有产生进位到符号位。
- C_in_msb = 0, C_out_msb = 0。两者匹配。
- 结果的符号位 = B + 0 + 0 = 0 + 0 + 0 = 0。结果仍然是正数。
- 这相当于两个 k-1 位的无符号数相加,其结果没有超出 k-1 位。一切正常。
- 情况二: B = 1 (溢出)
- 从数值部分产生了一个进位 1 到符号位。
- C_in_msb = 1, C_out_msb = 0。两者不匹配。
- 结果的符号位 = B + 0 + 0 = 1 + 0 + 0 = 1。
- 这意味着,两个正数相加,结果的符号位却变成了 1,即计算机认为结果是一个负数。这是错误的。
- 这就是“正+正=负”型的溢出。
- 示例1: 4位, 3+2=5 (不溢出)
- X=0011, Y=0010。
- 数值部分 011+010 = 101。没有产生进位。所以 B = C_in_msb = 0。
- 符号位加法 B+0+0 = 0+0+0 = 0。结果的符号位是0,没有向外进位。所以 A = C_out_msb = 0。
- A == B (0==0)。不溢出。结果 0101 (5)。正确。
- 示例2: 4位, 5+4=9 (溢出)
- X=0101, Y=0100。
- 数值部分 101+100 = (1)001。产生了一个进位。所以 B = C_in_msb = 1。
- 符号位加法 B+0+0 = 1+0+0 = 1。结果的符号位是1,没有向外进位。所以 A = C_out_msb = 0。
- A != B (0!=1)。溢出。结果 1001 (-7)。错误。
- 原文符号混乱: 原文的A和B定义似乎与标准用法有出入,容易造成混淆。在我的解释中,我将 A 明确为 C_out_msb,B 明确为 C_in_msb,这更清晰。
- 证明的逻辑: 证明的核心是把k位的加法拆分成“数值部分(k-1位)的加法”和“符号位的加法”两部分来分析。
本节证明了对于两个正数的2的补码加法:
- 溢出的充要条件是:低(k-1)位的数值部分加法产生了向符号位的进位。
- 这个条件等价于“进入符号位的进位为1,从符号位出去的进位为0”,即 C_in_msb=1, C_out_msb=0。
- 这个条件也等价于“两个正数相加,结果为负数”。
提供严谨的数学证明,以支持上一节提出的“进位不匹配即溢出”和“符号不符即溢出”的规则。通过分情况讨论,让这些规则的来源变得清晰可见,而不仅仅是死记硬背的结论。
正数区的“溢出”:
- 想象2的补码的环形数轴,0到 $2^{k-1}-1$ 是正数区。
- 两个正数相加,就像从一个正数点出发,再顺时针走几步。
- 如果不溢出,你仍然停留在正数区。
- 如果溢出,说明你走得太远了,越过了正数区的边界($2^{k-1}-1$),“掉进”了负数区。你停下的第一个负数点就是最小的负数(-2^{k-1})。
- 这个“越过边界”的动作,在硬件上就体现为数值部分向符号位产生了进位 1,把原本是 0 的符号位“污染”成了 1。
想象一个透明的量杯,有一半的高度被涂成了红色(负数区),一半是无色的(正数区)。
- 两个正数相加,就像往杯子里倒了两杯无色的水。
- 不溢出: 水位上升了,但还在无色区域。
- 溢出: 水倒得太多了,水位超过了无色区的顶端,进入了红色区域。虽然你倒的都是“正”的水,但最终的水位线却在“负”的区域里。那个“溢过”分界线的动作,就是 C_in_msb = 1。
211.2. 情况2:两者皆负
📜 [原文19]
- 情况 2:两者皆负:
- 写下两个最高位进位为 A 和 B
- $A=$ 进位 B $+1+1$
- A 始终为 1!
- 最高位 = B + 1 + 1
- $B=0$:最高位 = 0:正数 \#?错误
- $B=1$:负数:正常(并且 $\bmod 2^{\mathrm{k}}$ 正确)
这部分继续证明,讨论第二种情况:两个负数相加。
- 设定:
- 我们有两个 k 位的2的补码负数 X 和 Y。
- 因为是负数,它们的最高位(MSB)都是 1。
- X = 1 X_{k-2} ... X_0
- Y = 1 Y_{k-2} ... Y_0
- 同样,A 代表 C_out_msb,B 代表 C_in_msb。
- 分析 A (C_out_msb):
- 最高位的加法涉及到 X和Y的符号位(都是1)以及从数值部分传来的进位B。
- 所以最高位的加法是 B + 1 + 1。
- B+1+1 等于 B+2。在二进制里,2是10。
- 所以 B+1+1 的结果是:和为 B,进位为 1。
- 因此,A (从最高位出去的进位) 始终为1!
- C_out_msb (即A) = 1。
- 分析 B (C_in_msb):
- B 仍然是数值部分(低 k-1 位)加法产生的进位,可能是0或1。
- 结合分析,判断溢出:
- 我们已经确定 A = C_out_msb = 1。
- 溢出规则是 A != B。
- 所以,当两个负数相加时,溢出发生的条件是 1 != B,即 B = 0。
- 不溢出的条件是 A == B,即 B = 1。
- 解读两种情况:
- 情况一: B = 1 (不溢出)
- 从数值部分产生了一个进位 1 到符号位。
- C_in_msb = 1, C_out_msb = 1。两者匹配。
- 结果的符号位 = (B+1+1) 的和 = (1+1+1) 的和 = 1。结果仍然是负数。
- 一切正常。结果在模$2^k$下是正确的,并且也在表示范围内。
- 情况二: B = 0 (溢出)
- 从数值部分没有产生进位到符号位。
- C_in_msb = 0, C_out_msb = 1。两者不匹配。
- 结果的符号位 = (B+1+1) 的和 = (0+1+1) 的和 = 0。
- 这意味着,两个负数相加,结果的符号位却变成了 0,即计算机认为结果是一个正数。这是错误的。
- 这就是“负+负=正”型的溢出。
- 示例1: 4位, -3+(-2)=-5 (不溢出)
- X=-3 (1101), Y=-2 (1110)。
- 数值部分 101+110 = (1)011。产生了一个进位。所以 B = C_in_msb = 1。
- 符号位加法 B+1+1 = 1+1+1 = 11 (二进制)。结果的符号位是1,向外进位是1。所以 A = C_out_msb = 1。
- A == B (1==1)。不溢出。结果 1011 (-5)。正确。
- 示例2: 4位, -6+(-5)=-11 (溢出)
- X=-6 (1010), Y=-5 (1011)。
- 数值部分 010+011 = 101。没有产生进位。所以 B = C_in_msb = 0。
- 符号位加法 B+1+1 = 0+1+1 = 10 (二进制)。结果的符号位是0,向外进位是1。所以 A = C_out_msb = 1。
- A != B (1!=0)。溢出。结果 0101 (+5)。错误。
- 对 A=1 的理解: 两个负数相加,从符号位一定会产生一个进位出去。这本身是正常的,不代表溢出。是否溢出,取决于这个出去的进位 (A) 是否和进来的进位 (B) 相等。
- 负数世界的环绕: 负+负溢出,可以理解为在环形数轴上,从一个负数点出发,逆时针走得太远,越过了负数区的边界(如-8),“掉进”了正数区。
本节证明了对于两个负数的2的补码加法:
- 溢出的充要条件是:低(k-1)位的数值部分加法没有产生向符号位的进位。
- 这个条件等价于“进入符号位的进位为0,从符号位出去的进位为1”,即 C_in_msb=0, C_out_msb=1。
- 这个条件也等价于“两个负数相加,结果为正数”。
这是对溢出检测规则证明的第二部分,与前一节共同构成了一个完整的证明链条,解释了为什么“同号相加,结果异号”是溢出的标志。
负数区的“溢出”:
- 在2的补码环形数轴上,负数区通常在左半边。
- 两个负数相加,就像从一个负数点出发,再逆时针走几步。
- 不溢出: 你仍然停留在负数区。
- 溢出: 你逆时针走得太远了,越过了负数区的边界(最小负数,如-8),“掉进”了正数区的尾部(如+7)。
- 这个“越过边界”的动作,在硬件上就体现为:符号位 1+1 产生的进位 1 “跑了出去” (C_out=1),但数值部分又不够“大”来提供一个进位(C_in=0)去“填补”符号位,导致符号位变成了0。
回到那个红/无色量杯。
- 两个负数相加,就像往杯子红区的液面下,注入了两管“制冷剂”(让液面下降)。
- 不溢出: 液面下降了,但还在红色区域。
- 溢出: 制冷剂加得太多了,液面降得太低,穿过了红色区的底部,进入了无色区域。虽然你加的都是“负”的制冷剂,但最终的水位线却在“正”的区域里。那个“穿过”底线的动作,就是 C_in_msb=0 (数值部分没啥动静) 和 C_out_msb=1 (符号位自己搞出了大新闻) 的不匹配。
311.3. 情况3:一正一负
📜 [原文20]
- 情况 3:一个正数,另一个负数:
- 写下两个最高位进位为 $A$ 和 $B+X_{k-2} X_{k-3} \ldots X_{0}$
- $A=$ 进位 $(B+1): B=0 \rightarrow A=0, B=1 \rightarrow A=1 \quad 1 Y_{k-2} Y_{k-3} \ldots Y_{0}$
- 所以永远不会溢出?
- 没错!
- 注意 $X+(-Y)$ 将小于 $X$ 且大于 $-Y$
- 如果 $X$ 可以用 2 的补码表示,并且 $-Y$ 可以用 2 的补码表示,那么任何 $Z$ 在 $-Y \leq Z \leq X$ 之间也都可以表示。
这是证明的最后一种情况:一个正数和一个负数相加。
- 设定:
- 我们有一个正数 X 和一个负数 Y。
- X 的MSB是 0,Y 的MSB是 1。
- X = 0 X_{k-2} ... X_0
- Y = 1 Y_{k-2} ... Y_0
- A = C_out_msb,B = C_in_msb。
- 分析 A (C_out_msb) 和 B (C_in_msb) 的关系:
- 最高位的加法是 B + 0 + 1,这里的0和1是X和Y的符号位。
- 最高位的计算是 B + 1。
- 结果的符号位是 (B+1)的和。
- A (从最高位出去的进位) 是 (B+1)的进位。
- 我们来分析 B 和 A 的关系:
- 如果 B=0 (数值部分没进位),那么 B+1 = 0+1 = 1。和是1,进位是0。所以 A=0。在这种情况下,A==B。
- 如果 B=1 (数值部分有进位),那么 B+1 = 1+1 = 10 (二进制)。和是0,进位是1。所以 A=1。在这种情况下,A==B。
- 结论: 无论 B 是0还是1,我们总是有 A = B!即 C_out_msb 永远等于 C_in_msb。
- 最终结论:
- 因为溢出的条件是 A != B,而我们证明了在这种情况下 A 永远等于 B。
- 所以,“所以永远不会溢出?没错!”
- 逻辑上的解释:
- 为什么一正一负相加永不溢出?
- 设正数为 P > 0,负数为 N < 0。它们的和是 S = P + N。
- 因为 N 是负数,所以 S = P + N < P。
- 因为 P 是正数,所以 S = P + N > N。
- 所以,和 S 的值一定介于 N 和 P 之间 (N < S < P)。
- P 和 N 本身都在可表示的范围内。任何介于两个可表示的数之间的数,也必然是可表示的。(这里有一个小小的例外,即当 P 是最大正数,N 是最小负数时,但它们的和通常接近0,远不会溢出)。
- 既然数学结果 S 永远在可表示的范围内,根据定义,就永远不会发生溢出。
- 示例1: 4位, 5+(-3)=2
- X=5 (0101), Y=-3 (1101)。
- 数值部分 101+101 = (1)010。B = C_in_msb = 1。
- 符号位加法 B+0+1 = 1+0+1 = 10。结果符号位是0,向外进位是1。A = C_out_msb = 1。
- A == B (1==1)。不溢出。结果 0010 (2)。正确。
- 示例2: 4位, 7+(-2)=5
- X=7 (0111), Y=-2 (1110)。
- 数值部分 111+110 = (1)101。B = C_in_msb = 1。
- 符号位加法 B+0+1 = 1+0+1 = 10。结果符号位是0,向外进位是1。A = C_out_msb = 1。
- A == B (1==1)。不溢出。结果 0101 (5)。正确。
- 示例3: 4位, -8+7=-1
- X=-8 (1000), Y=7 (0111)。
- 数值部分 000+111 = 111。B = C_in_msb = 0。
- 符号位加法 B+1+0 = 0+1+0 = 1。结果符号位是1,向外进位是0。A = C_out_msb = 0。
- A == B (0==0)。不溢出。结果 1111 (-1)。正确。
- 直觉陷阱: 有人可能会觉得一个很大的正数加上一个很小的负数(绝对值小),结果可能会溢出。但证明告诉我们,这是不可能的。因为结果只会比那个大正数小一点,离溢出边界反而更远了。
- 减法: A - B,如果A和B符号相同,等价于一正一负相加,永不溢出。如果A和B符号不同(正-负 或 负-正),等价于同号相加,就有可能溢出。
本节完成了溢出检测规则证明的最后一步,证明了当一个正数和一个负数相加时,C_in_msb 总是等于 C_out_msb,因此永远不会发生溢出。结合前两节,我们完整地证明了2的补码加法溢出的充要条件是“两个同号的数相加,得到了一个不同符号的结果”。
提供一个全面、严谨的证明,消除对溢出检测规则的所有疑虑。它构成了计算机算术理论的坚实基础。
在环形数轴上,一正一负相加,就像从一个正数点出发,逆时针走几步(或者从一个负数点出发,顺时针走几步)。这个操作本质上是在两个点之间“折返跑”,你永远不会跑到两个端点之外的区域,所以永远不会“掉出”表示范围。
你站在一座桥上(数轴),桥的一头是“正数村”,另一头是“负数村”,中间是0点。
- 两个正数相加:从正数村向更远的正数方向走,有可能走得太远掉下桥(正向溢出)。
- 两个负数相加:从负数村向更远的负数方向走,有可能走得太远掉下桥(负向溢出)。
- 一正一负相加:你从正数村的某处出发,掉头往负数村方向走(或者反过来)。你的整个移动轨迹都在桥面之上,绝无可能掉下桥。
1212. 关于溢出的最后思考
112.1. 溢出示例分析
📜 [原文21]
- 不能过分强调溢出意味着结果无法在字长内表示(不一定是结果太大)!
- 示例:假设我选择一个(奇怪的)方式将 2-位字映射到值,如下所示:
| 两位字 word |
关联值 Value |
|---|---|
| 00 | 1 |
| 01 | 3 |
| 10 | 6 |
| 11 | 2 |
因此,对于此表示,00+01 导致溢出
这部分通过一个非常规的、人为设计的例子,来回归和强调溢出最根本的定义。
- 核心论点: 溢出的本质是“结果无法在当前表示法下表示”,而不一定是因为结果“太大”或“太小”。它完全取决于你如何定义二进制模式与数值之间的映射关系。
- 奇怪的表示法:
- 我们抛弃所有前面学的标准表示法,自己发明一个。
- 用2个位,我们有4个模式:00, 01, 10, 11。
- 我们规定它们的映射关系是:
- 00 -> 1
- 01 -> 3
- 10 -> 6
- 11 -> 2
- 这个表示法所能表示的数值集合是 {1, 2, 3, 6}。
- 在这个表示法下进行运算:
- 示例1: 1 + 1
- 1 对应的二进制是 00。
- 所以 1+1 对应于二进制加法 00 + 00。
- 00 + 00 = 00。
- 等等,原文写的是 00+00=11。这说明这个奇怪的系统里,连加法器(BAA)都被修改了!它可能是一个自定义的逻辑。但我们先假设加法器还是标准的BAA。
- 00 + 00 = 00。结果 00 对应的值是 1。
- 数学上 1+1=2。计算机结果是 1。结果不符。
- 让我们采信原文的 00+00=11。这意味着这个系统的“加法规则”是自定义的。根据这个规则,00和00相加,结果的二进制模式是11。
- 11 在我们的表示法里对应的值是 2。
- 数学上 1+1=2。计算机结果是 2。在这种自定义加法下,1+1 没有溢出。
- 示例2: 1 + 3
- 1 对应的二进制是 00。
- 3 对应的二进制是 01。
- 数学上的和应该是 1 + 3 = 4。
- 关键问题: 在我们的表示法 {1, 2, 3, 6} 中,有没有 4 这个值?没有。
- 结论: 因为数学结果 4 无法用我们这套奇怪的表示法来表示,所以 1+3 这个运算,在这个系统里,必然导致溢出。
- 无论 00 + 01 的二进制结果是什么(是01也好,是10也好,或其他),它解读出来的值(3 或 6)都不等于 4。
- 示例: 在这个奇怪的系统里计算 3+3
- 3 对应 01。
- 数学结果: 3 + 3 = 6。
- 检查表示范围: {1, 2, 3, 6}。6 在范围内!
- 所以 3+3 有可能不溢出,前提是二进制加法的结果必须正确地得到 10。
- 假设使用标准BAA: 01 + 01 = 10。
- 10 在我们的表示法里对应的值是 6。
- 计算机结果 6 和数学结果 6 相符。所以,3+3 在这个系统里不溢出。
- 默认标准表示法: 我们太习惯于无符号和2的补码了,以至于会下意识地认为溢出就是“大于最大值”或“小于最小值”。这个例子提醒我们,溢出的定义更具普遍性。
- 表示范围的“空洞”: 这个奇怪的表示法 {1, 2, 3, 6} 是不连续的,它中间有“空洞”(缺少0, 4, 5)。任何运算结果如果恰好掉在这些空洞里,就是溢出。
本节通过一个极端的人造例子,回归了溢出最根本的定义:当且仅当一个运算的精确数学结果,不在当前表示法所能表示的数值集合之内时,该运算发生溢出。这与结果是否“太大”或“太小”没有必然联系,完全取决于表示法的定义。
目的是为了打破思维定势,加深对溢出本质的理解。通过展示一个“反直觉”的例子,它促使我们从最第一性的原理出发去思考问题,而不是仅仅依赖于在标准表示法下总结出的规则(如“正+正=负”)。
你有一台只能显示特定单词的打字机。
- 表示法: 你的打字机只能打出 {"CAT", "DOG", "PIG", "COW"} 这四个词。
- 运算: 你在做一个填字游戏,"C" + "A" + "T" 应该得到 "CAT"。
- 不溢出: 游戏的结果是 "DOG",你的打字机可以打出来。
- 溢出: 游戏的结果是 "BIRD"。但你的打字机根本没有 "BIRD" 这个键。你想打出结果,但是做不到。这就是溢出。问题不在于 "BIRD" 是一个特别长或特别短的词,仅仅是因为它“不在你的词汇表里”。
你有一个自动售货机,它只卖四种饮料:可乐(1号按钮),雪碧(2号按钮),芬达(3号按钮),橙汁(6号按钮)。
- 表示法: {可乐, 雪碧, 芬达, 橙汁} 对应 {1, 3, 6, 2}。
- 你想买一杯“奶茶”(值=4)。
- 你站在售货机前,发现根本没有“奶茶”这个选项。
- 你的购买行为“溢出”了,因为你想要的东西,这台机器不提供。
1313. 浮点
113.1. 需要更大的范围?浮点表示
📜 [原文22]
- 改变编码。
- 浮点(用于以紧凑方式表示非常大的数字)
- 很像科学记数法:
尾数
注意:尾数总是采用 X.XX... 形式
(又名小数部分)
(小数点前一位)
这一部分标志着从整数表示到浮点数表示的过渡。前面讨论的所有整数表示法,无论是无符号还是2的补码,都存在一个共同的局限性:对于固定的位数(如32位),它们能表示的数值范围是有限的,并且无法表示小数。
- 问题背景: 如果我们需要表示非常大(如宇宙的质量)或非常小(如电子的质量)的数字,或者需要表示带有小数部分的数字(如π=3.14159...),那么固定位数的整数表示法就不够用了。即使是64位的long long,也只能表示到 $10^{18}$ 左右,这在科学计算中是远远不够的。
- 解决方案: “改变编码”。我们不再让每一位都代表一个固定的权重(如$2^0, 2^1, 2^2...$),而是采用一种更灵活的编码方式——浮点(Floating-Point)。
- 核心思想:科学记数法: 浮点表示法的核心思想借鉴了我们都熟悉的科学记数法。
- 在十进制科学记数法中,任何一个数都可以表示成 A × 10^B 的形式。
- A 被称为尾数 (Mantissa) 或有效数 (Significand)。
- 10 是基数 (Base)。
- B 是指数 (Exponent)。
- 示例: -7776 可以写成 -7.776 × 10^3。
- 这里的 - 是符号。
- 7.776 是尾数。
- 10 是基数。
- 3 是指数。
- 通过调整指数 B 的大小,我们可以让小数点“浮动”起来,从而表示范围极广的数字。例如,1.23 × 10^30 是一个巨大的数,1.23 × 10^-30 是一个极小的数。
- 尾数的规范化 (Normalization):
- “尾数总是采用 X.XX... 形式(小数点前一位)”。
- 这是一个重要的约定,称为规范化。在十进制科学记数法中,我们通常要求尾数的整数部分是一个非零的个位数,即 1 ≤ |A| < 10。
- 例如,123 不会写成 123 × 10^0 或 0.123 × 10^3,而是规范地写成 1.23 × 10^2。
- 这样做的好处是,对于任何一个非零数,其规范化的科学记数法表示是唯一的。这对于标准化存储和计算至关重要。
- -: 符号 (Sign)。表示这个数是负数。
- 7.776: 尾数 (Mantissa)。它携带了数字的“有效数字”。
- ×: 乘号。
- 10: 基数 (Base)。在十进制系统中,基数是10。
- 3: 指数 (Exponent)。它表示小数点需要移动多少位。正指数表示向右移动(数字变大),负指数表示向左移动(数字变小)。
- = -7776: 这是科学记数法表示的数的常规十进制形式。
- = -6^5: 这是一个补充说明,恰好-7776等于-6的5次方。这与浮点表示的核心思想关系不大,可能只是一个有趣的数学巧合。
- 示例1: 巨大的数
- 地球的质量大约是 5,972,000,000,000,000,000,000,000 千克。
- 用科学记数法表示为 $5.972 \times 10^{24}$ 千克。
- 这里,符号是正(省略),尾数是5.972,指数是24。用这种方式,我们只用了几个数字就简洁地表示了一个极大的量。
- 示例2: 微小的数
- 一个水分子的质量大约是 0.0000000000000000000000299 克。
- 用科学记数法表示为 $2.99 \times 10^{-23}$ 克。
- 这里,尾数是2.99,指数是-23。
- 精度损失: 浮点表示法虽然范围广,但它的精度是有限的。尾数的位数决定了它能表示多少位有效数字。例如,如果尾数只能存3位有效数字,那么 1.2345 × 10^10 就会被近似为 1.23 × 10^10,损失了 0.0045 × 10^10 的信息。这是浮点数与理想实数最大的区别。
- 基数: 我们习惯于基数为10的科学记数法。但计算机是二进制的,所以计算机内的浮点表示法,其基数是2。
本节介绍了浮点表示法的基本思想,它通过借鉴十进制的科学记数法,将一个数拆分为符号、尾数和指数三部分来表示。这种方法允许用固定的位数(例如32位或64位)来表示一个范围极广且包含小数的数值集合,从而克服了整数表示法的局限性。
本节的目的是为了引入一种全新的数字编码方案,以解决整数表示法无法处理小数和极大/极小数的问题。它是后续所有关于浮点数标准(IEEE 754)、运算、精度和误差等讨论的开端。
- 整数表示法: 就像一把刻度均匀的尺子。每个刻度之间的距离都是1。尺子的总长度是固定的。
- 浮点表示法: 像一个“可伸缩的”尺子,或者说是一个尺子加上一个放大镜。
- 尾数: 是尺子本身,但它很短,只有有限的几个刻度(决定了精度)。
- 指数: 是放大镜的倍数。
- 当你看一个很远、很大的物体时,你用一个高倍率的放大镜(大指数),尺子上的一个小小刻度可能就代表一千米。
- 当你看一个很近、很小的物体时,你用一个更高倍率的放大镜(负指数),尺子上的一个刻度可能只代表一微米。
- 通过改变放大镜的倍率(指数),这把短尺子(尾数)可以测量各种尺度的东西。
你正在给一个巨大的城市绘制地图。
- 整数画法: 你想用1厘米代表1米。但城市太大了,你的纸(固定的位数)根本画不下。
- 浮点画法: 你在地图旁边加了一个“比例尺”说明。
- 画市中心时,你的比例尺是“1厘米 = 10米”(小指数)。
- 画整个城市轮廓时,你的比例尺是“1厘米 = 10公里”(大指数)。
- 尾数: 就是你在图上画的那些线条的长度。
- 指数: 就是那个比例尺。
- 通过改变比例尺,你在同一张纸上既能画出建筑的细节,又能画出整个城市的宏观布局。
213.2. 浮点表示示例
📜 [原文23]
- 但对于本课程,请考虑二进制:
注意:在正确形式中,对于二进制,尾数总是 1.XX... (小数点前一位,且该位总是 1)
唯一例外:$0=0.0 \times 2^{0}$
这一部分将上一节介绍的通用科学记数法思想,具体应用到计算机的二进制世界中。
- 从十进制到二进制: 计算机不使用基数10,它使用基数2。所以,浮点数的通用形式从 A × 10^B 变成了 A × 2^B,其中 A 和 B 也都是用二进制表示的。
- 二进制浮点数示例:
- -1.10 × 2^0111
- 符号: -,是负数。
- 尾数 (Mantissa): 1.10。这是一个二进制小数。它的值是 $1 \cdot 2^0 + 1 \cdot 2^{-1} + 0 \cdot 2^{-2} = 1 + 0.5 + 0 = 1.5$ (十进制)。
- 基数 (Base): 2。
- 指数 (Exponent): 0111。这是一个二进制整数。它的值是 $0 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 = 4 + 2 + 1 = 7$ (十进制)。
- 整合: 整个数的值是 -1.5 × 2^7。
- 计算: 2^7 = 128。所以值是 -1.5 × 128 = -192。
- 二进制的规范化:
- “在正确形式中,对于二进制,尾数总是 1.XX... ”。
- 这对应于十进制科学记数法中要求尾数 1 ≤ |A| < 10 的规则。在二进制中,任何一个非零数,我们都可以调整其指数,使得其尾数的整数部分为 1。
- 例如,一个二进制数 10110.1。
- 它可以写成 10110.1 × 2^0。
- 为了规范化,我们把小数点向左移动4位,变成 1.01101。
- 每向左移动一位,相当于除以2,所以指数需要加1。移动4位,指数就加4。
- 所以,规范化的形式是 1.01101 × 2^4。
- 为什么总是1.XX...? 因为在一个二进制数中,最高位的非零位必然是 1。我们总是可以移动小数点,让它紧跟在这个最高的1后面。
- 隐含位 (Implicit Bit) 的思想:
- 既然对于任何非零数,规范化后的尾数第一位总是1,那我们还有必要在内存里专门花一个比特来存储这个1吗?
- 答案是没必要。我们可以约定,在存储时,我们只存储小数点后面的部分(XX...),而在计算时,由硬件自动在前面“补”上那个 1.。
- 这个被省略的、但大家都心知肚明的 1,被称为“隐含位”或“隐藏位”(Hidden Bit)。这是IEEE 754标准中的一个关键优化,它使得在相同的位数下,尾数的精度可以凭空多出一位。
- 唯一的例外:
- 数字 0 是一个例外。0 无法写成 1.XX... 的形式。
- 因此,需要一个特殊的表示来处理 0。在IEEE 754标准中,当指数和尾数的所有位都为0时,表示的数就是0。
- -: 符号,负。
- 1.10: 二进制尾数。. 是二进制小数点(radix point)。
- 1 在小数点左边,权重是 $2^0=1$。
- 第一个 1 在小数点右边,权重是 $2^{-1}=0.5$。
- 0 在小数点右边第二位,权重是 $2^{-2}=0.25$。
- 所以 1.10 (bin) = $1 \times 1 + 1 \times 0.5 + 0 \times 0.25 = 1.5$ (dec)。
- 2: 二进制基数。
- 0111: 二进制指数。
- 0111 (bin) = $0 \cdot 8 + 1 \cdot 4 + 1 \cdot 2 + 1 \cdot 1 = 7$ (dec)。
- 等式右边是对左边二进制形式的十进制翻译。
- 示例1: 表示十进制数 9.75
- 步骤1: 整数和小数部分分开转二进制。
- 9 (dec) = 1001 (bin)。
- 0.75 (dec) = 0.5 + 0.25 = $1 \cdot 2^{-1} + 1 \cdot 2^{-2}$ = .11 (bin)。
- 所以 9.75 (dec) = 1001.11 (bin)。
- 步骤2: 规范化。
- 1001.11,小数点需要向左移动3位,才能变成 1.00111。
- 所以规范化形式是 1.00111 × 2^3。
- 符号:正。尾数:1.00111。指数:3。
- 示例2: 解读二进制浮点数 +1.01 × 2^-2
- 符号:正。
- 尾数:1.01 (bin) = $1 + 0 \cdot 0.5 + 1 \cdot 0.25 = 1.25$ (dec)。
- 指数:-2 (dec)。
- 值 = 1.25 × 2^-2 = 1.25 × 0.25 = 0.3125 (dec)。
- 二进制小数转换: 十进制小数转二进制小数采用“乘2取整法”,容易出错。十进制有限小数,转成二进制可能是无限循环小数(例如 0.1 (dec))。这是浮点数精度问题的根源之一。
- 忘记隐含位: 在分析实际的浮点数内存布局时(如下一节的IEEE 754),初学者常常忘记计算时要把那个“隐藏的1”加回来。
- 0的处理: 0是一个需要特殊规则处理的边界情况。
本节将浮点表示的核心思想从十进制平移到了二进制。关键知识点包括:1) 形式为尾数 × 2^指数;2) 二进制的规范化形式是 1.XX...;3) 这个1.可以被省略以节省空间(隐含位思想);4) 数字0是唯一的例外,需要特殊处理。
本节是连接“科学记数法”这个通用概念和“IEEE 754标准”这个具体实现的桥梁。它解释了为什么IEEE 754标准会设计成后面我们将要看到的样子,特别是“隐含位”这个设计的理论基础。
“隐含位”心智模型:
- 这就像一个俱乐部,会员卡上只需要印你的名字的后半部分。因为所有会员的姓都一样,比如姓“王”。所以卡上印着“二小”,大家自动知道你叫“王二小”。这个“王”就是隐含位。
- 这样做的好处是,在同样大小的卡片上可以印更长的名字,比如“麻子”,大家知道你叫“王麻子”。精度更高了。
- 唯一的例外是俱乐部的创始人,他不姓王,他就叫“零”。他的卡是空白的,需要特殊识别。
想象你在写一本关于所有非零数字的“族谱”。
- 你发现,所有数字,无论高矮胖瘦,追根溯源,都可以通过乘以或除以足够多次2,变成一个“始祖”的形式,这个“始祖”的大小在1到2之间(不含2)。
- 例如,12 -> 6 -> 3 -> 1.5。它的始祖是1.5。
- -0.25 -> -0.5 -> -1.0。它的始祖是1.0。
- 这个“始祖”就是规范化的尾数,它的形式永远是 1.XXX。
- 浮点表示法就是记录两件事:1. 这个数字的“始祖”长什么样(尾数的小数部分)。2. 它和“始祖”差了多少代(指数)。
1414. 浮点数的标准形式
📜 [原文24]
- 如何在 32-位字的限制内表示浮点数
- 字的位分成不同的字段
3130292827262524232221201918171615141312111009080706050403020100
符号 小数部分 (尾数)
- IEEE 754 标准规定
- 哪些位表示哪些字段(位 31 是符号位,位 30-23 是 8-位指数,位 22-00 是 23-位小数部分)
- 如何解释每个字段
这一部分正式引入了工业界和学术界广泛采用的浮点数标准——IEEE 754。它规定了如何在一个32位的二进制字中,为符号、指数和尾数这三部分信息“划分地盘”。
- 问题: 我们有一个32位的存储空间(比如一个float类型的变量),需要把一个浮点数的所有信息(符号、指数、尾数)都塞进去。如何合理分配这32个比特?
- 解决方案:分字段 (Fields):
- 我们将32个比特分成三个独立的字段,每个字段负责存储一部分信息。
- 符号 (Sign): 只需要1位。0代表正,1代表负。
- 指数 (Exponent): 需要一些位来存储指数的大小。
- 小数部分 (Fraction) / 尾数 (Mantissa): 需要最多的位来存储有效数字,这直接决定了精度。
- IEEE 754 单精度 (32-bit) 标准:
- 这是一个国际标准,确保了在所有遵循该标准的计算机上,浮点数的表示和运算都是一致的。这对于软件的可移植性至关重要。
- 地盘划分规则:
- 位 31 (最高位): 1位,用作符号位 (S)。
- 位 30-23: 8位,用作指数位 (E)。
- 位 22-0: 23位,用作小数部分 (F)。
- 可视化:
- 解释规则:
- 标准不仅规定了位的划分,还规定了如何解释每个字段的值,以及如何将它们组合成最终的数值。这将在下一节详细展开。
- 示例: 编码十进制数 9.75
- 在上一节,我们知道 9.75 的规范化二进制形式是 +1.00111 × 2^3。
- 现在我们要把它编码成 IEEE 754 格式:
- 符号 (S): 正数,所以 S = 0。
- 指数 (E): 指数是 3。IEEE 754使用一种“偏移表示法”(下一节会讲),对于8位指数,偏移量是127。所以存储的指数值是 实际指数 + 偏移量 = 3 + 127 = 130。
- 130 (dec) = 10000010 (bin)。所以8位指数场 E = 10000010。
- 小数部分 (F): 规范化的尾数是 1.00111。我们省略掉隐含的1.,只存储小数部分 00111。这23位的小数部分字段需要填满,所以我们在后面补0。
- F = 00111000000000000000000。
- 组合: 将S, E, F拼接起来:
```
S E F
0 10000010 00111000000000000000000
```
- 这个32位的二进制模式就是在IEEE 754标准下 9.75 在内存中的实际样子。
- 字段顺序: 必须记清楚 S-E-F 的顺序,以及每个字段的位数。最高位是符号,然后是指数,然后是小数。
- 尾数 vs 小数部分: 术语上容易混淆。尾数 (Mantissa/Significand) 通常指完整的 1.F 部分。而小数部分 (Fraction) F 是指存储在23位字段里的那部分。Significand = 1 + Fraction。
- 指数不是直接存储的: 这是一个巨大的易错点。8位指数场 E 存储的不是实际的指数值(如3),而是加上一个偏移量(127)之后的值。
本节介绍了浮点数的业界标准——IEEE 754(以32位单精度为例)。它将一个32位的字划分成三个字段:1位的符号、8位的指数和23位的小数部分。这个标准化的“地盘划分”方案是实现可移植、可交互的浮点计算的基础。
目的是将浮点表示从一个抽象的概念,落实到一个具体的、标准化的硬件实现方案上。它回答了“在实践中,计算机是如何组织一个浮点数的32个比特的?”这个问题,为后续解码和编码浮点数打下了结构基础。
IEEE 754 就像一张标准化的“数字身份证”。
- 32位字: 身份证的卡片大小。
- 符号字段: “性别”栏(1位:男/女)。
- 指数字段: “出生年代”栏(8位:可以表示不同的年代,如80后、90后...)。
- 小数部分字段: “个人照片”栏(23位:提供了主要的个人身份信息)。
- 有了这张标准身份证,任何一个“读卡器”(CPU)都能正确地读取和识别这个人的信息。
你正在打包一个快递,快递单有三个标准化的格子。
- 第一个小格子 (S): 只能打一个勾,选项是“普通件”或“加急件”。
- 第二个中等格子 (E): 填写“距离等级”,比如“同城”、“省内”、“国内”、“国际”等,这个等级决定了邮费的基数。
- 第三个大格子 (F): 填写详细的物品描述。
- IEEE 754标准就是这张快递单的设计规范。它规定了每个格子的大小、位置和填写内容的格式,确保任何一个快递站都能看懂。
1515. IEEE 754 浮点描述
📜 [原文25]
3130292827262524232221201918171615141312111009080706050403020100
| $\frac{5}{5}$ | 指数 | 小数部分 (尾数) |
|---|
- 符号:0 = 正数 \#,1 = 负数 \#(像有符号幅度)
- 指数:无符号,偏移量为 127
- 指数值 = 8 位无符号二进制表示 -127
- 小数部分:回想小数部分总是 1.XXXXXX 形式
- 省略‘1’,只表示“XXXXXXX”部分
3130292827262524232221201918171615141312111009080706050403020100
1000011011010000000000000000000
- $=(-1) \times 1.101_{(2)} \times 2^{13-127}=-1.625_{(10)} \times 2^{-114}=-7.82409 \times 10^{-35}$
- 因为表示总是 $\pm 1.\mathrm{XXXX} \times 2^{\text{yyy}}$ 形式,不能表示真正的 0
- 注意:所有位都设为 0 等于 $1.0 \times 2^{-127}$,一个非常非常小的数字,实际上是 0
这一部分详细解释了IEEE 754标准中每个字段的解码规则,并通过一个完整的例子演示了如何将一个32位的二进制模式转换成它所代表的十进制数。
- 解码规则:
- 符号 (S):
- 位于位31。
- 0 代表正数,1 代表负数。这和有符号幅度表示法是一样的。
- 最终值的计算公式里,可以用 (-1)^S 来表示符号。
- 指数 (E):
- 位于位30-23,共8位。
- 它本身被当作一个无符号整数来解读,范围是 0 到 255。
- 偏移表示法 (Biased Representation): 存储的指数 E 并不是真正的指数。实际的指数值 e 需要通过 e = E - bias 来计算。
- 对于单精度(32位),这个偏移量 (bias) 固定为 127。
- 所以,实际指数 = 存储的8位无符号值 - 127。
- 为什么用偏移表示法? (下一节会讲),主要是为了简化比较操作。
- 小数部分 (F):
- 位于位22-0,共23位。
- 它存储的是规范化尾数 1.XXX... 中,小数点后面的部分。
- 在计算时,我们需要把那个被省略的“隐含位 1”给补回来。
- 所以,完整的尾数 (Significand, M) 的值是 1 + F。这里的 F 是把23位小数部分当作二进制小数来计算的值。例如,如果 F = 1010...,那么它的值是 $1 \cdot 2^{-1} + 0 \cdot 2^{-2} + 1 \cdot 2^{-3} + ...$。
- 完整解码公式 (对于规范化数):
Value = (-1)^S × (1 + F) × 2^(E - 127)
- 示例解码:
- 二进制模式: 1 0000110 11010000000000000000000
- 分解:
- S = 1 (符号为负)。
- E = 00001101 (bin)。作为无符号数,它的值是 $8+4+1 = 13$ (dec)。
- F = 110100...0 (bin)。
- 计算:
- (-1)^S = (-1)^1 = -1。
- 实际指数 e = E - 127 = 13 - 127 = -114。
- 小数部分 F 的值是 $1\cdot2^{-1} + 1\cdot2^{-2} + 0\cdot2^{-3} + 1\cdot2^{-4} = 0.5 + 0.25 + 0.0625 = 0.8125`。
- 尾数 M = 1 + F = 1 + 0.8125 = 1.8125。
- 等等,原文的计算是 1.101。让我看看 F=1101...。 1.F 应该是 1.1101。1.1101 (bin) = $1+0.5+0.25+0.0625 = 1.8125$。原文中的1.101可能是笔误,或者它省略了F的某个1。让我们按照原文的 1.101 来算,这意味 F 应该是 1010...。1.101(bin) = $1+0.5+0.125=1.625$。这与原文的-1.625吻合。所以我们假设 F 字段实际上是 1010...,而 E 是 00001101 (13)。
- 按照原文的 1.101 和 E=13 重新计算:
- Value = -1 × 1.625 × 2^(13 - 127)
- Value = -1.625 × 2^-114。
- $2^{-114}$ 是一个极小的数,约等于 $4.85 \times 10^{-35}$。
- 所以最终值约等于 -1.625 × 4.85e-35 ≈ -7.88e-35。这与原文的 -7.82409e-35 基本一致(差异可能来自计算器精度或原文数字的微小笔误)。
- 关于0的讨论:
- “因为表示总是 $\pm 1.\mathrm{XXXX} \times 2^{\text{yyy}}$ 形式,不能表示真正的 0”。这个公式是针对规范化数的。在这种形式下,因为尾数 1+F 永远大于等于1,所以结果永远不可能是0。
- “注意:所有位都设为 0 等于 $1.0 \times 2^{-127}$,一个非常非常小的数字,实际上是 0”。
- 这句话描述了一个矛盾,并暗示了我们目前的知识不完整。
- 如果我们严格按照上面的规范化公式,当S=0, E=0, F=0时,Value = (-1)^0 × (1+0) × 2^(0-127) = 1.0 × 2^-127。这是一个非常接近0的数,但不是0。
- 这说明,IEEE 754 标准中有一些特殊规则。事实上,当指数字段 E 全为0时,它就进入了一种称为“非规范化数 (Denormalized Numbers)”的模式,此时隐含位不再是1而是0,并且指数的计算也不同。而当E和F都全为0时,它就明确地定义为0。这些特殊情况处理了0和下溢问题。原文在这里只是埋下伏笔。
- $=(-1) \times 1.101_{(2)} \times 2^{13-127}=-1.625_{(10)} \times 2^{-114}=-7.82409 \times 10^{-35}$
- (-1): 来自符号位 S=1。
- 1.101 (2): 尾数 M = 1+F。这里的 (2) 下标表示它是二进制。它的十进制值是1.625。
- 2: 基数。
- 13-127: 实际指数 e = E - bias。E=13, bias=127。
- -1.625 (10): 是 -1.101 (2) 的十进制翻译。
- 2^-114: 指数部分。
- -7.82409 x 10^-35: 整个浮点数的近似十进制值。
- 指数偏移: 最常见的错误是忘记指数的偏移量 127。直接把 E 当作指数来用是错误的。
- 隐含位: 第二大易错点是忘记在计算尾数值时补上 1.。
- 特殊值: IEEE 754 标准不仅定义了规范化数,还为 0, 无穷大(Infinity), 非数(NaN) 以及非常小的非规范化数定义了特殊的编码规则。这些通常是通过预留一些特殊的指数字段值(如全0或全1)来实现的。本节的讨论只涵盖了最常见的“规范化数”情况。
本节详细阐述了如何解码一个标准的32位IEEE 754浮点数。核心解码公式为 Value = (-1)^S × (1 + F) × 2^(E - 127)。通过一个具体例子,我们实践了从一个32位二进制模式中分离出S, E, F三个字段,并根据规则计算出其最终代表的十进制值的全过程。同时,本节也暗示了标准中存在处理0等特殊值的额外规则。
提供解码IEEE 754浮点数的具体操作指南。这是将浮点理论付诸实践的关键一步。掌握了这个解码过程,就能从根本上理解float类型变量在内存中的本质,以及浮点数运算可能出现的各种现象(如精度损失、舍入误差等)。
解码IEEE 754浮点数就像解读一份加密情报。
- 32位码: 加密的情报原文。
- 解码手册 (IEEE 754):
- 第一条规则:看第1个字符,是'A'就是我方,是'B'就是敌方 (S 字段)。
- 第二条规则:看第2到第9个字符,把它转换成数字,再减去127,就知道行动的“日期” (E 字段)。
- 第三条规则:看剩下的字符,在它前面加个“1.”,就知道行动的“具体内容” (F 字段和隐含位)。
- 只有严格按照手册,才能正确解读情报。
你有一个神奇的调味瓶。瓶子上有三个调节旋钮。
- S旋钮: 只有两档,“盐”或“糖”。
- E旋钮: 8位,刻度从0到255。它控制调味料的“浓度等级”,但刻度是偏移的,127档才是“标准浓度”,128档是“2倍浓度”,126档是“半倍浓度”。
- F旋钮: 23位,非常精密。它控制调味料的“基础风味”,比如“微辣”、“中辣”、“变态辣”。
- 一个32位的浮点数,就是这三个旋钮的一组特定设置。把它们组合起来,就能调制出成千上万种不同的味道(数值)。
1616. 偏移量和浮点数比较
116.1. 步骤2:检查指数
📜 [原文26]
- 偏移量允许指数在 -127(非常小)和 128(非常大)之间
- 问:为什么使用偏移量而不是 2 的补码或无符号幅度?
- 答:比较两个浮点数 A & B 哪个更大很容易
- 步骤 1:检查符号。A 为正,B 为负,返回 A > B。A 为负,B 为正,返回 A < B
- 步骤 2 (A 和 B 符号相同): 检查指数
- (A 为正且 A.指数 > B.指数) 或 (A 为负且 A.指数 < B.指数),返回 A > B
- (A 为负且 A.指数 > B.指数) 或 (A 为正且 A.指数 < B.指数),返回 A < B
这一部分解释了在浮点数的指数部分采用偏移表示法(Biased Representation)的一个核心原因:它极大地简化了浮点数大小的比较。
- 指数范围:
- 8位的指数字段 E,作为无符号数范围是 0 到 255。
- 实际指数 e = E - 127。
- 所以 e 的范围是 0-127 到 255-127,即 -127 到 +128。(注意:E=0 和 E=255 是为特殊值保留的,所以实际规范化数的指数范围是 -126 到 +127)。这允许我们表示极大和极小的数。
- 核心问题: 为什么指数不使用我们熟悉的2的补码来表示正负,而要用这个看起来有点绕的偏移表示法?
- 核心答案: 为了让浮点数的比较可以像整数比较一样直接。如果把整个32位的浮点数当作一个32位的整数(忽略其浮点含义)来比较大小,我们希望其比较结果能和它所代表的浮点值的比较结果保持一致。偏移表示法帮助我们实现了这一点。
- 比较步骤:
- 步骤1: 比较符号位 (S)
- 这是最优先的。如果一个数是正 (S=0),另一个是负 (S=1),那么正数显然更大。这和整数比较中,正数总大于负数是一样的。
- 步骤2: 比较指数位 (E)
- 当两个浮点数符号相同时,我们需要进一步比较它们的幅度。浮点数的幅度主要由指数决定。指数越大的数,其幅度通常也越大。
- 关键点: 因为我们用了偏移表示法,一个更大的实际指数 e 会对应一个更大的存储指数 E。例如,e1=5, e2=10。E1=5+127=132, E2=10+127=137。e2 > e1 对应 E2 > E1。
- 这意味着,我们可以直接比较8位的指数字段 E 的无符号大小,来判断其实际指数 e 的大小。
- 如果用2的补码会怎样? e1=5 (00000101), e2=-10 (11110110)。如果当成无符号整数比较,11110110 > 00000101,我们会错误地认为-10比5大。偏移表示法避免了这个问题。
- 分情况讨论:
- 两个都为正数: S相同(都为0)。此时,指数 E 越大的数,值越大。所以 A.E > B.E 意味着 A > B。
- 两个都为负数: S相同(都为1)。此时,情况相反。指数 E 越大的数,其幅度(绝对值)越大,但因为它是个负数,所以它的实际值反而更小。例如 -100 的幅度比 -10 大,但 -100 < -10。所以 A.E > B.E 意味着 A < B。
- 原文的描述 (A 为正且 A.指数 > B.指数) 或 (A 为负且 A.指数 < B.指数),返回 A > B 是对这个逻辑的总结。
- 示例: 比较 A = 12.0 和 B = 8.0
- A = 12.0 = 1.1 × 2^3。S=0, e=3, E=130 (10000010), F=100...
- B = 8.0 = 1.0 × 2^3。S=0, e=3, E=130 (10000010), F=000...
- 步骤1: S_A = 0, S_B = 0。符号相同,都是正数。
- 步骤2: E_A = 130, E_B = 130。指数相同。
- (进入下一节的步骤3)
- 示例: 比较 A = 100.0 和 B = 10.0
- A = 100.0 ≈ 1.1001 × 2^6。S=0, e=6, E=133 (10000101)。
- B = 10.0 = 1.01 × 2^3。S=0, e=3, E=130 (10000010)。
- 步骤1: S_A=0, S_B=0。都是正数。
- 步骤2: E_A = 133, E_B = 130。因为是正数,E_A > E_B,所以直接得出结论 A > B。我们甚至不需要看小数部分。
- 示例: 比较 A = -100.0 和 B = -10.0
- A = -100.0。S=1, e=6, E=133。
- B = -10.0。S=1, e=3, E=130。
- 步骤1: S_A=1, S_B=1。都是负数。
- 步骤2: E_A = 133, E_B = 130。E_A > E_B。因为是负数,指数大的反而值更小。所以 A < B。
- 忘记负数情况反转: 在比较两个负的浮点数时,很容易想当然地认为指数大的数更大,但实际正好相反。
- 比较的本质: 这种分步比较的方法,完美地映射到“将整个32位字当成一个整数来比较”的行为上(对于正数)。一个32位的正浮点数 A,如果把它看成一个32位无符号整数 I_A,另一个正浮点数 B 看作 I_B,那么 A > B 当且仅当 I_A > I_B。这就是设计的精妙之处。对于负数,这个整数比较的规则是相反的。
本节解释了浮点数指数部分采用偏移表示法的关键原因:它使得浮点数的比较操作可以被极大地简化。通过直接比较存储的指数字段 E 的大小,就可以快速判断两个浮点数的主要量级关系,这为硬件实现快速比较提供了便利。
回答一个“为什么”的问题。2的补码对于整数来说如此优秀,为什么在浮点数的指数部分却弃用了它?本节给出了答案:为了“比较”的效率。这展示了在计算机体系结构设计中,不存在一成不变的“最优”方案,而是需要根据具体目标(是简化加减法,还是简化比较)来做出权衡和选择。
- 2的补码:像一个钟表,-1 (11...1) 和 0 (00...0) 是邻居,但从无符号整数来看,它们一个最大,一个最小,序关系完全乱了。
- 偏移表示法: 像给所有人都加上一个固定的“年龄”,比如127岁。
- 一个实际-1岁的人,记录为126岁。
- 一个实际+10岁的人,记录为137岁。
- 这样,所有人的“记录年龄”都是正数,并且他们“记录年龄”的大小关系和他们“实际年龄”的大小关系是完全一致的。比较“记录年龄”就能知道谁大谁小,非常直接。
你在整理一个图书馆的书,书上有两个标签:一个是实际的出版年份(可以是公元前,即负数),另一个是图书馆的入库编号。
- 2的补码方式: 你把公元1年编为1号,公元前1年编为-1号的2的补码。这样,一本公元前1年的书(-1,11...1)和一本公元1年的书(1, 00...01)在书架上会离得很远,编号看起来也完全没关系。
- 偏移表示法方式: 你规定一个“基准年”,比如公元2000年。所有书的入库编号都是 出版年份 + 2000。
- 公元2010年的书,编号是 2010+2000=4010。
- 公元前100年(-100)的书,编号是 -100+2000=1900。
- 现在,你只需要看入库编号,编号越大的书,出版年份就越晚。排序和比较变得非常容易。
216.2. 步骤3:检查小数部分
📜 [原文27]
- 步骤 3 (A 和 B 符号相同,指数相同): 检查小数部分
- (A 为正且 A.小数部分 > B.小数部分) 或 (A 为负且 A.小数部分 < B.小数部分),返回 A > B
- (A 为负且 A.小数部分 > B.小数部分) 或 (A 为正且 A.小数部分 < B.小数部分),返回 A < B
这是浮点数比较流程的第三步,当前提是两个数的符号和指数都相同时,我们需要通过比较小数部分来一决高下。
- 前提: 我们正在比较A和B,并且已经确定:
- A.S == B.S (符号相同)
- A.E == B.E (指数相同)
- 这意味着两个数在同一个数量级上,我们需要观察它们的“有效数字”部分来区分大小。
- 比较小数部分 (F):
- 小数部分字段 F 存储了尾数的精度信息。
- 由于隐含的1.是相同的,比较完整的尾数 1+A.F 和 1+B.F 的大小,就等价于直接比较小数部分 A.F 和 B.F 的大小。
- F 字段是一个23位的二进制串,我们可以直接把它当作一个23位的无符号整数来比较大小。
- 分情况讨论:
- 两个都为正数:
- 符号和指数都相同,那么尾数更大的数,其值就更大。
- A.F > B.F 意味着 1+A.F > 1+B.F,所以 A > B。
- 两个都为负数:
- 符号和指数都相同,尾数更大的数,其幅度(绝对值)更大,但由于是负数,其值反而更小。
- A.F > B.F 意味着 |A| > |B|,所以 A < B。
- 反之,A.F < B.F 意味着 |A| < |B|,所以 A > B。
- 原文的逻辑 (A 为正且 A.小数部分 > B.小数部分) 或 (A 为负且 A.小数部分 < B.小数部分),返回 A > B 正是这个思想的体现。
- 示例1: 比较 A = 12.0 和 B = 10.0
- A = 12.0 = 1.100 × 2^3。 S=0, E=130, F = 100...
- B = 10.0 = 1.010 × 2^3。 S=0, E=130, F = 010...
- 步骤1: 符号相同 (正)。
- 步骤2: 指数相同 (130)。
- 步骤3: 比较小数部分F。
- A.F = 100...
- B.F = 010...
- 把它们当成无符号整数比较,显然 100... > 010...。
- 因为是正数,所以 A > B。
- 示例2: 比较 A = -12.0 和 B = -10.0
- A = -12.0。 S=1, E=130, F = 100...
- B = -10.0。 S=1, E=130, F = 010...
- 步骤1: 符号相同 (负)。
- 步骤2: 指数相同 (130)。
- 步骤3: 比较小数部分F。
- A.F = 100...
- B.F = 010...
- A.F > B.F。
- 因为是负数,小数部分(即幅度)大的反而值更小。
- 所以 A < B。
- F的比较: 比较F时,就是从左到右逐位比较,第一个出现不同的位就能决定大小,和比较普通整数一样。
- 整数比较的映射: 将 S-E-F 字段拼接起来,对于正数,可以直接作为一个32位整数来比较大小。S是最高位,E是次高位,F是最低位,它们的排列顺序保证了整数比较的结果和浮点比较的结果一致。这正是IEEE 754设计的精妙之处!
本节阐述了浮点数比较的第三步:当符号和指数都相同时,通过比较小数部分 F 字段的大小来确定最终结果。对于正数,F 大的数更大;对于负数,F 大的数反而更小。
这是对浮点数比较逻辑的补充,处理了当两个数数量级相同时的情况。至此,我们已经有了一套完整的比较任意两个(规范化)浮点数的流程。
你正在比较两本书的“价值”。
- 步骤1 (符号): 一本是“资产”,一本是“负债”。“资产”价值更高。
- 步骤2 (指数): 两本都是“资产”,一本是“明朝古籍”,一本是“现代小说”。“明朝古籍”的年代更久远(指数差异大),价值可能更高。
- 步骤3 (小数部分): 两本都是“明朝古籍”,出版年份也一样。你需要仔细看书的内容、品相、印刷(小数部分F)来判断哪一本更珍贵。品相更好的(F更大),价值更高。
- 如果两本都是“负债”(比如欠款合同),年份也一样。那么品相更好的(F更大,意味着欠款数额的有效数字更大),其“价值”就更低(因为是负债)。
比较两个人的身高。
- 步骤1: 忽略。
- 步骤2 (指数): 一个人身高是“米”级别的(指数大),另一个是“厘米”级别的(指数小)。米级别的更高。
- 步骤3 (小数部分): 两个人都是1米多(指数相同)。一个身高1.85米,一个身高1.75米。你需要比较小数点后的数字85和75(小数部分F),85 > 75,所以第一个人更高。
316.3. 步骤4:完全相等与有符号比较的相似性
📜 [原文28]
- 步骤 4 (A 和 B 符号相同,指数相同,小数部分相同): 返回 A = B
- 观察:当位按照符号、指数、幅度排序时,过程与比较 2 个有符号幅度数相同
哪个 IEEE 754 FP \# 最大?

- 所有 + \#s,$B > A$(指数更大),$B > C$(指数相同,小数部分更大)
- 如果 \#s 简单地视为有符号幅度,会怎样?
- 结果相同:$B > C > A$
这一部分是浮点数比较的最后一步和总结,并提出了一个深刻的观察,将浮点数比较与一种我们熟悉的整数表示法联系起来。
- 步骤4: 完全相等:
- 如果比较到了这一步,意味着A和B的符号(S)、指数(E)和小数部分(F)三个字段的二进制模式完全相同。
- 那么,这两个浮点数就是相等的。A = B。
- (注意:这里忽略了+0和-0的问题。在IEEE 754中,S=0, E=0, F=0 和 S=1, E=0, F=0 表示的+0和-0,它们的二进制位不同,但通常被认为是“相等”的,这需要特殊处理)。
- 核心观察: “当位按照符号、指数、幅度排序时,过程与比较 2 个有符号幅度数相同”。
- 这句话是本节的点睛之笔。让我们来解构它。
- “位按照符号、指数、幅度排序”: IEEE 754标准正好就是这么做的!最高位是符号(S),接下来是指数(E),最后是小数部分(F),F决定了尾数的幅度。
- “有符号幅度数”: 回忆一下有符号幅度整数表示法。它也是最高位是符号,其余位是幅度。
- 比较过程的相似性:
- 比较有符号幅度数时,我们先看符号。一正一负,正大。
- 如果符号相同,我们再比较后面的幅度位。对于正数,幅度大的数大;对于负数,幅度大的数小。
- 这和我们刚刚分步骤讨论的浮点数比较流程,在逻辑上是完全一样的!
- S 对应 有符号幅度的符号位。
- E 和 F 拼接起来,就像是有符号幅度的幅度部分。因为E在高位,F在低位,所以E起决定性作用,E相同时才看F。
- 这个观察的意义:
- 这意味着,对于正的浮点数,我们可以把它的32位二进制模式直接当作一个32位的无符号整数(或者正的有符号整数)来比较大小!硬件上只需要一个整数比较器就能完成浮点数比较,极其高效。
- 例如,A > B (A, B都为正) iff (unsigned int)A > (unsigned int)B。
- 这就是为什么指数要用偏移表示法。它保证了指数部分E的整数大小顺序和实际指数e的大小顺序一致,从而让整个32位字可以被“整体地”当作整数来比较。
- 图片示例分析:
- 给出了三个正的浮点数 A, B, C。
- A: 0 011... 101...
- B: 0 100... 011...
- C: 0 100... 110...
- 比较 B 和 A: 都是正数。B的指数 100... 大于 A的指数 011...。所以 B > A。
- 比较 B 和 C: 都是正数。指数相同 100...。比较小数部分,C的 110... 大于 B的 011...。所以 C > B。(等等,我看的图可能和原文想表达的不一致,原文结论是 B > C)
- 按原文结论 B>C 分析: 那么应该是 B 的小数部分 011... 比 C 的 110... 要大。这不可能。所以原文结论B>C可能有误,或者我对图的解读有误。让我们假设C的小数部分是001...,那么 B(011...) > C(001...) 成立。
- 让我们重新看原文结论: "$B > A$(指数更大),$B > C$(指数相同,小数部分更大)"。这说明在 B 和 C 之间,B的小数部分更大。所以我们接受这个设定。
- 最终排序: C > B > A 或者 B > C > A (取决于B和C的F谁大)。重点是比较的逻辑。
- 如果视为有符号幅度数:
- 把S当作符号,E和F拼接起来当作幅度。
- A, B, C都是正数。我们只需比较 E:F 这一整长串二进制的大小。
- B的E比A大,所以 B > A。
- B和C的E相同,如果B的F比C大,那么 B > C。
- 比较结果和浮点比较完全一样!B > C > A。
- 负数的情况: 对于负数,这个“整数比较”的规则是相反的。A > B (A,B都为负) iff (unsigned int)A < (unsigned int)B。
- 特殊值: NaN (非数) 的比较行为很特殊。任何涉及NaN的比较(除了 !=)都返回false。例如 NaN == NaN 是false。
本节是浮点数比较的收尾和升华。它指出了浮点数在完全相同时的判断条件,并揭示了IEEE 754标准设计的精髓:通过巧妙地安排S, E, F字段的顺序,并为E采用偏移表示法,使得浮点数的比较可以被映射为硬件上非常快速的整数比较。
本节的目的是揭示浮点数表示法背后的深刻设计思想。它告诉我们,一个好的标准,不仅要能正确地表示数据,还要考虑到对这些数据进行操作(如比较)的效率。IEEE 754正是这种软硬件协同设计的典范。
IEEE 754浮点数的二进制布局,就像一个精心设计过的“字典序”。
- S (符号): 就像单词的首字母,是排序的第一关键字。所有首字母为'A'-'M'的词(正数)都排在首字母为'N'-'Z'的词(负数)前面。
- E (指数): 就像单词的第二个字母,是排序的第二关键字。
- F (小数): 就像单词剩下的部分,是最后的排序依据。
- 因为
这种精心设计的排序,使得硬件可以用一个通用的、非常快速的整数比较器来处理绝大多数浮点数的比较,而不需要一个专门的、复杂的浮点比较单元。
你有一套按“姓-名”规则排序的卡片。
- 符号(S) 是“姓”。
- 指数(E) 是名字的“第一个字”。
- 小数(F) 是名字的“第二个字及以后”。
- 比较两张卡片A和B的顺序,你自然会:
- 先比较“姓”。姓在字母表前面(比如‘A’姓 vs ‘Z’姓)的排前面。
- 如果姓一样,再比较名字的“第一个字”。
- 如果第一个字也一样,再比较“第二个字”。
- 这个过程和你查字典的顺序完全一样。IEEE 754把浮点数变成了可以用“查字典”的方式(即整数比较)来排序的格式,大大提高了效率。
1717. IEEE 754 64-位 (双精度)
📜 [原文29]
- 在 32-位架构中描述为两个 32-位字
| 字 1 | 31/30292827262524232221201918171615141312111009080706050403020100 | |
|---|---|---|
| 指数 | 小数部分 (高位) |
3130292827262524232221201918171615141312111009080706050403020100
字 2 小数部分 (低位)
- 11-位指数,偏移量为 1023
- 小数部分长 52 位(字 1 中 20 个高位,字 2 中剩余 32 个低位)
这一部分介绍了IEEE 754标准的另一种常见格式:64位双精度(Double Precision),在C语言中对应double类型。它提供了比32位单精度更高的精度和更广的表示范围。
- 需求背景: 32位的单精度浮点数虽然范围比整数大得多,但其精度有限(大约7位十进制有效数字)。在许多科学计算、金融建模等领域,这点精度是远远不够的,计算过程中微小的舍入误差会累积起来,导致最终结果出现巨大偏差。因此,需要一种更高精度的浮点格式。
- 64位双精度:
- 它使用64个比特(8个字节)来表示一个浮点数。
- 在一些老的32位架构中,由于硬件一次只能处理32位,一个64位的double可能被存储在两个相邻的32位内存单元(“字”)中。现代64位架构则可以原生处理64位数据。
- 这64位的“地盘划分”与32位类似,但每个字段的位数都增加了:
- 符号 (S): 仍然是1位(位63)。
- 指数 (E): 扩展到11位(位62-52)。
- 小数部分 (F): 扩展到52位(位51-0)。
- 双精度的解码规则:
- 符号 (S): 规则不变,0为正,1为负。
- 指数 (E):
- 因为有11位,所以E的无符号取值范围是 0 到 2^11 - 1 = 2047。
- 偏移量 (bias) 也相应增大了,变为 1023。
- 所以,实际指数 e = E - 1023。
- 规范化数的实际指数范围是 1 - 1023 到 2046 - 1023,即 -1022 到 +1023。范围远超单精度的 -126 到 +127。
- 小数部分 (F):
- 有52位用于存储小数部分。
- 加上1位的隐含位,尾数的总精度达到了53位。
- $2^{53}$ 约等于 $9 \times 10^{15}$。这意味着双精度浮点数大约有15-17位十进制有效数字,远高于单精度的7位。
- 原文表格的解读:
- 原文的表格描述了一种在32位系统上如何“拼凑”出64位双精度数的情景。
- 字1: 存储了高位的32个比特。这32位里又被细分:
- 位31是符号S。
- 位30-20是11位指数E。(原文这里似乎有误,30-20只有11位,但图上标到了23,我们以11位为准)
- 位19-0是52位小数部分F的“高20位”。
- 字2: 存储了低位的32个比特,全部用于表示小数部分F的“低32位”。
- 20 (高位) + 32 (低位) = 52位小数部分。这个描述是自洽的。
- 这种分两个字存储的方式在现代64位系统中已不常见,但它有助于理解双精度数各个部分的构成。
- 示例: 编码十进制数 -192.0
- -192.0 = -1.5 × 128 = -1.5 × 2^7。
- 规范化二进制形式是 -1.1 × 2^7。
- 符号 (S): 负数, S = 1。
- 指数 (E): 实际指数 e=7。双精度的偏移量是1023。
- E = e + 1023 = 7 + 1023 = 1030。
- 1030 (dec) = 1024 + 6 = 10000000110 (bin)。这是11位的指数。
- 小数部分 (F): 尾数是 1.1。小数部分是 .1。
- F 需要填满52位,所以是 1000...0 (一个1后面跟51个0)。
- 组合: S=1, E=10000000110, F=100...0。
- 单精度与双精度的混淆: 在编程和计算时,必须清楚地区分float(单精度)和double(双精度)。它们的位数、范围、精度和偏移量都完全不同。
- 偏移量: 双精度的偏移量是1023,而不是单精度的127。
- 特殊值: 双精度同样有为0, 无穷大, NaN等保留的特殊指数值(E全为0或全为1)。
本节介绍了IEEE 754标准的64位双精度浮点格式。它通过将位数扩展到64位(1位符号,11位指数,52位小数),实现了比32位单精度高得多的精度(约16位十进制有效数字)和更广的表示范围。其编码原理(符号、偏移指数、隐含位)与单精度一脉相承,只是各项参数有所不同。
目的是介绍在实际应用中更常用、更精确的double类型所对应的底层标准。这让学习者明白,单精度和双精度并非两种完全不同的东西,而是同一设计思想在不同资源(位数)投入下的两种实现。
如果说单精度float是一张标准的“身份证”,那么双精度double就是一本“护照”。
- 卡片大小: 护照(64位)比身份证(32位)厚得多。
- 性别栏 (S): 都有,还是1位。
- 出生年代栏 (E): 护照上的这个栏位更长(11位),不仅能记录“90后”,还能记录到更精确的“92年8月生”,表示范围更广。
- 个人照片栏 (F): 护照上的照片更大、更清晰(52位),能看清脸上的每一颗痣,提供了更多的细节信息(精度更高)。
回到画地图的例子。
- 单精度: 是用一张A4纸画地图,比例尺选项比较有限,画出的细节也比较粗糙。
- 双精度: 是用一张巨大的A1画纸画地图,比例尺选项非常丰富,可以画得极为精细。
- 用A4纸(单精度)画整个世界地图,可能只能标出国家。而用A1画纸(双精度),不仅能标出国家,甚至能画出城市里的主要街道。
1818. 下溢
📜 [原文30]
- 当值的幅度太小而无法用表示形式描述时
- 例如,在 IEEE 754 浮点中:
- $X = 1 \times 2^{-100}$ 可以通过标准表示(指数字段中的位集是什么?)
- 但是,$X^2$ 等于 $2^{-200}$ 太小,无法表示
- 最小可能指数是 -127
- 因此,尝试计算 $X*X$ 会导致下溢
这一部分介绍与溢出(Overflow)相对的概念——下溢(Underflow)。
- 下溢的定义: “当值的幅度太小而无法用表示形式描述时”。
- 溢出 (Overflow) 是指数值太大,超出了正数或负数的表示范围的“上界”。
- 下溢 (Underflow) 是指数值太小(即负得太多),导致整个数的幅度(绝对值)极其接近于零,超出了表示范围的“下界”。
- 它描述的是一个数“小到无法分辨”,而不是“负到无法表示”。
- 示例分析 (单精度浮点数):
- 单精度浮点数的最小规范化指数是 e_min = 1 - 127 = -126。所以能表示的最小正规范化数是 $1.0 \times 2^{-126}$。
- X = 1.0 × 2^-100: 这个数可以表示。
- 符号 S = 0。
- 尾数 M = 1.0,所以小数部分 F = 0。
- 实际指数 e = -100。存储指数 E = e + 127 = -100 + 127 = 27。
- 27 (dec) = 00011011 (bin)。这在8位E的范围内。
- 所以 X 可以被精确表示。
- 计算 X * X:
- X^2 = (1.0 × 2^-100)^2 = 1.0^2 × (2^-100)^2 = 1.0 × 2^-200。
- 检查是否可以表示:
- 我们需要表示的实际指数是 e = -200。
- 单精度浮点数能表示的最小(最负)的规范化指数是 -126。(原文写的-127是E=0时的特殊情况,我们先按规范化数理解)。
- -200 远远小于 -126。
- 所以,1.0 × 2^-200 这个值,它的幅度太小了,无法用标准的规范化浮点数来表示。
- 结论: 计算 X*X 会导致下溢。
- 下溢后的结果:
- 当下溢发生时,计算结果会怎么样?
- 最简单的处理方式是直接将结果视为 0。这被称为“突变到零”(Flush to Zero)。
- IEEE 754标准提供了一种更优雅的处理方式,即使用前面提到的“非规范化数”(Denormalized Numbers)。当指数 E 全为0时,系统进入非规范化模式,此时可以表示比最小规范化数更小的数,实现了从最小规范化数到0的“渐进下溢”(Gradual Underflow)。这避免了 a-b=0 当且仅当 a=b 这种重要数学性质在计算机中失效的问题。但这是一个更高级的主题。对于本课程的理解,可以暂时认为下溢的结果就是0。
- 示例1: 单精度
- 最小的正规范化数 min_norm = 1.0 × 2^-126。
- 如果我们计算 min_norm / 2.0,数学结果是 1.0 × 2^-127。
- 这个结果的指数 -127 已经超出了规范化数的表示范围,发生了下溢。
- 在支持渐进下溢的系统中,这个结果会被表示成一个非规范化数 0.5 × 2^-126(它的指数域E为0,小数域F不为0)。
- 在只支持突变到零的系统中,这个结果会直接变成 0.0。
- 示例2: 双精度
- 双精度的最小规范化指数是 e_min = 1 - 1023 = -1022。
- 最小正规范化数是 1.0 × 2^-1022。
- 如果我们计算 (1.0 × 2^-600) * (1.0 × 2^-600),结果是 1.0 × 2^-1200。
- -1200 小于 -1022,所以这个计算在双精度下也会发生下溢。
- 下溢 vs 负溢出: 下溢是幅度太小(趋近于0),而整数的负溢出是数值太小(负得太多)。例如,8位2的补码计算-100 + (-100) 得到正数,是负溢出。1e-20 * 1e-20 结果变成0,是下溢。
- 0的精确性: 下溢的存在意味着,在浮点运算中,一个计算结果等于0,并不一定意味着数学上的结果就精确为0,它可能只是一个非常小、但非零的数因为下溢而被“冲刷”成了0。
本节介绍了下溢的概念,它与溢出相对,指的是一个数的幅度(绝对值)小到无法用浮点表示法表示的现象。当计算结果的实际指数小于所能表示的最小指数时,就会发生下溢。下溢的结果通常被处理为0或一个特殊的非规范化数。
为了完整地描述浮点数表示范围的局限性。浮点数既有“上界”(最大值,超出则溢出),也有“下界”(最接近0的非零值,小于则下溢)。理解下溢对于编写数值稳定性好的科学计算程序非常重要。
回到“可伸缩的尺子+放大镜”模型。
- 溢出: 你想测量的物体(比如银河系)太大了,即使你用了最小倍率的放大镜(最大的正指数),物体在你的尺子上还是“爆框”了。
- 下溢: 你想测量的物体(比如一个原子)太小了,即使你用了最大倍率的放大镜(最小的负指数),这个物体在你的尺子上仍然显示不出任何长度,看起来就像一个点。它的尺寸已经超出了你的测量工具的“分辨率下限”。
你有一台电子秤。
- 溢出: 你想称一头大象的重量,但它的重量超过了秤的量程(比如最大150公斤)。秤的显示屏可能会显示 "Error" 或者一个乱码。
- 下溢: 你想称一根羽毛的重量。你把羽毛放上去,但秤的读数仍然是 "0.00" 公斤。不是因为羽毛没有重量,而是因为它的重量太小了,低于这台秤的“最小感量”。羽毛的重量“下溢”了。
1919. 讲座结束
📜 [原文31]
- 课程其余部分的重要要点:
- 计算机的高层视角(数字化视角):字长这一概念
- 二进制数:负数表示法(二进制补码)
- 加法、减法、溢出、溢出检测
这部分是本次元件或讲座的总结,提炼出了最重要的、需要在后续课程中牢记的核心概念。
- 计算机的高层视角(数字化视角):字长
- 数字化视角: 这是理解计算机工作原理的根本出发点。计算机将所有信息——数字、文字、图像、声音——都转换成二进制数字(比特序列)来处理。这个过程就是数字化。
- 字长 (Word Size): 计算机在一次操作中能够处理的二进制位的基本单位。例如,一个32位处理器,其字长就是32位。字长是计算机体系结构的一个核心参数,它直接决定了CPU的寄存器大小、内存寻址空间以及默认的整数运算范围。它是连接硬件能力和软件数据类型的桥梁。
- 二进制数:负数表示法(二进制补码)
- 在二进制世界里,如何表示负数是一个核心问题。
- 我们学习了多种方法(有符号幅度、1的补码),但最终聚焦于2的补码。
- 2的补码之所以重要,是因为它只有一个0,充分利用了所有位模式,并且极大地简化了加减法运算的硬件实现。它是现代计算机表示有符号整数的事实标准。
- 加法、减法、溢出、溢出检测
- 这是计算机算术的核心。
- 加法/减法: 在2的补码体系下,减法可以统一为加法(A - B = A + (-B)),使得硬件只需要一个加法器。
- 溢出 (Overflow): 算术运算的一个固有风险。当计算结果超出了当前字长和表示法所能定义的范围时发生。
- 溢出检测: 硬件必须有能力检测到溢出的发生,以便软件可以进行相应的处理。我们学习了无符号和2的补码下不同的、高效的溢出检测方法(前者看Carry Flag,后者看符号或进位匹配)。
这三大要点构成了本讲座的知识主干。它们从计算机的根本抽象(数字化和字长),到具体的数据表示(2的补码),再到对这些数据的核心操作(算术运算及其边界情况),形成了一个完整的逻辑链条。掌握这些知识是深入学习计算机组成原理、操作系统、编译器等后续课程的基础。
本节的目的是为学习者“划重点”。在吸收了大量细节知识之后,一个清晰的、高度概括的总结有助于巩固核心概念,形成知识体系,并指明这些知识在未来学习路径中的重要性。
2020. 行间公式索引
- 二进制加法示例 (5 + (-3))
这个公式展示了在4位2的补码下,计算 5 + (-3) 的过程,结果正确地得到2。
- 2的补码加法溢出示例 (7+7)
这个公式展示了在4位2的补码下,计算 7+7 如何导致溢出,最终得到错误结果-2。
- 自定义表示法下的运算与溢出
这个公式在一个非标准的2位表示法下,演示了 1+1=2 (不溢出) 和 1+3=4 (结果无法表示,导致溢出) 的情况。
- 十进制科学记数法示例
这个公式用科学记数法表示了数字-7776,作为引入浮点数思想的例子。
- 二进制浮点数表示示例
这个公式展示了一个二进制浮点数的具体形式,并将其翻译成对应的十进制科学记数法。
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。